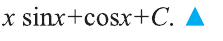Интегральные кривые векторных полей и потоки на многообразиях
В этом разделе мы рассмотрим несколько полезных понятий, тесно связанных
с определением и свойствами производной Ли.
Напомним, что гладкой параметризованной кривой
на многообразии
называется гладкое отображение
где
— интервал вещественной оси, который без ограничения общности
всегда можно выбрать единичным:
Переходя к координатам
многообразия в некоторой карте, через которую проходит кривая,
будем иметь систему функций
описывающих параметризованную кривую
в координатах этой карты. Здесь
— параметр на кривой.
На интервале
мы имеем постоянное векторное поле
— это векторный базис на
рассматриваемом как одномерное многообразие. Его перенос на кривую
посредством дифференциала отображения:
называется
векторным полем скорости на кривой
Кривая
называется регулярной, если
в каждой точке кривой
(в механической интепретации — нет точек остановки).
В координатах поле скорости задается выражением (проверьте!):
где точка сверху означает дифференцирование по параметру.
Рассмотрим гладкое векторное поле
на многообразии
Кривая
называется
интегральной кривой векторного поля
если в каждой точке кривой выполняется равенство:
где
— ограничение векторного поля
на кривую
определяемое по формуле:
для всякой функции
Уравнение (
30
) в координатах принимает вид системы обыкновенных дифференциальных уравнений:
Ее геометрический смысл заключается в коллинеарности векторов элементарных перемещений
(их линейных частей)
вдоль кривой и векторов векторного поля в соответствующих точках
кривой.
Записывая это условие коллинеарности в виде
6
:
приходим к т.н.
системе уравнений на характеристики векторного поля
т.е. такие
-мерные поверхности, которые “сотканы” из линий тока
векторного поля.
Уравнения характеристик появляются как совокупность интегралов системы (
32
):
где
— семейство констант интегрирования.
При фиксированных значениях констант
каждое уравнение из (
33
) определяет некоторую
характеристику в
а в совокупности пересечение
характеристик
определяет конкретную интегральную кривую поля
К такой конкретизации можно прийти,
потребовав, чтобы
эта кривая проходила через заданную точку
с координатами
при
В таком случае в систему (
33
) следует подставить
вместо
и разрешить ее относительно
После этого мы вместо (
33
) будем иметь систему вида:
которую можно разрешить относительно каких-то
переменных
(без ограничения общности
можно считать, что это первые
-переменных
):
Далее, подставляя полученные зависимости в уравнение:
получаем обыкновенное дифференциальное уравнение,
с разделяющимися переменными. Константу интегрирования следует выбрать так, чтобы
выполнялось начальное условие:
Теперь подставляя найденную зависимость
в уравнения (
34
),
получаем полное координатное описание интегральной кривой с необходимыми свойствами:
Рассмотрим следующий пример. Пусть
— векторное поле на плоскости
с координатами
Уравнение характеристик
имеет интеграл
const
Он описывает семейство окружностей различных радиусов
Если
то
и
Очевидно, что семейство интегральных кривых векторного поля
можно рассматривать
как отображение
:
которое каждую точку
смещает вдоль интегральной кривой,
проходящей через эту точку, причем при
это отображение является тождественным:
и при этом
Отображение
называется
потоком векторного поля
на многообразии
В силу общих теорем существования и единственности в некоторой окрестности любой неособой точки
гладкого векторного поля (т.е. точки, в которой
) поток
является диффеоморфизмом.
В окрестности особых точек векторного поля диффеоморфность отображения
может нарушаться.
Мы показали, что всякое гладкое (на самом деле достаточно непрерывности!) векторное поле
определяет поток на многообразии. Покажем, что всякому
потоку на многообразии, понимаемому как гладкое
отображение
:
соответствует векторное поле, которое его порождает.
Действительно, рассмотрим векторное поле:
В каждой точке многообразия, где определен поток, это поле определено и его
линии потока являются интегральными кривыми векторного поля
по определению (
30
).
Таким образом,
существует взаимно-однозначное соответствие между
векторными полями и потоками на гладком многообразии.
Рассмотрим в качестве примера поток на плоскости, задаваемый
в координатах соотношениями:
Соответствующее векторное поле получается дифференцированием этих соотношений по
и приравниванием
к нулю. В результате будем иметь:
Попробуйте изобразить это векторное поле стрелками на плоскости самостоятельно.
Такой поток осуществляет гиперболические (псевдоевклидовы) вращения плоскости.
След.:8. Производная Ли и Выше:Элементы геометрии гладких многообразий Пред.:6. Отображения многообразий и
Бсэ1/интегралы уравнений движения — викитека
ИНТЕГРАЛЫ УРАВНЕНИЙ ДВИЖЕНИЯ (механ.). И. у. д. обычно называют такие соотношения между мгновенными значениями величин, определяющих состояние движения, к-рые остаются неизменными во время движения (для механических систем величинами, определяющими состояние движения, являются координаты положения и составляющие скорости). В аналитической механике различают первые И. у. д., дающие соотношение между скоростями, координатами и временем, от вторых И. у. д., выражающих связь координат системы со временем. И. у. д. получаются в результате интегрирования системы дифференциальных уравнений движения.
Например, для научения движения одной материальной точки (центра масс) при задании действующих сил и массы необходимо решать следующую систему ур-ий:
где Xi{displaystyle X_{i}} — составляющие равнодействующей сил по осям координат — могут зависеть от времени t{displaystyle t}, координат xi{displaystyle x_{i}} и составляющих скорости dxidt{displaystyle {frac {dx_{i}}{dt}}}. Если удастся систему (1) представить в виде
| (2) |
то выражения φi{displaystyle varphi _{i}}, содержащие время, координаты, составляющие скорости и три произвольных постоянных интеграции
| (3) |
называются первыми И. у. д. В свою очередь, если система ур-ий (3) может быть заменена ей эквивалентной системой
| (4) |
то тогда выражения, содержащие время, координаты и шесть произвольных постоянных
называются вторыми И. у. д. Разрешая соотношения (5) относительно xk{displaystyle x_{k}} получим самые общие выражения для искомых функций, содержащие шесть произвольных постоянных
xi=Fi(t,C1,C2,C3,C4,C5,C6),(i=1,2,3){displaystyle x_{i}=F_{i}(t,C_{1},C_{2},C_{3},C_{4},C_{5},C_{6}),(i=1,2,3)}
Для системы, обладающей N степенями свободы (см.), число произвольных постоянных в первых И. у. д. равно N{displaystyle N}, а по вторых И. у. д. — 2N{displaystyle 2N}. Произвольные постоянные интеграции, обыкновенно, определяются из начальных условий, т. е. для какого-либо момента времени t=t0{displaystyle t=t_{0}} должны быть заданы координаты и составляющие скорости. К важнейшим первым И. у. д. относятся интегралы количества движения, интегралы момента количества движения или интегралы площадей и интеграл живых сил или — более обще — интеграл энергии.
Одним из наиболее важных И. у. д. классической механики является интеграл энергии, гласящий, что механическая энергия изолированной системы, равная сумме кинетической и потенциальной энергии, есть величина постоянная. В зависимости от того, допускает или не допускает система интеграл энергии, ее называют консервативной (см. Консервативное силовое поле, Механика) или неконсервативной. Ни одна макроскопическая система не является строго консервативной; работа всех машин и приборов сопровождается трением, в силу чего часть механической энергии пере-ходит в теплоту и консервативность нарушается. Далее часть энергии может перейти в другие, не рассматриваемые задачей виды энергии. Наконец, ни одна система в мире не является строго изолированной; поэтому для получения ответа на тот или иной вопрос нам приходится идеализировать рассматриваемые системы, считая их консервативными, — это возможно всегда, когда за интересующее нас время движение системы мало затухает в силу трения. Для изолированной механической системы, т. е. системы, на к-рую не действуют внешние силы (и в к-рой внутренние силы удовлетворяют закону равенства действия противодействию), кроме интеграла энергии, известны еще шесть фундаментальных интегралов; три интеграла сохранения количества движения (или скорости) центра тяжести и три интеграла площадей, выражающие постоянство трех составляющих вектора момента количества движения. Математическая формулировка указанных И. у. д. следующая: 1. Интеграл энергии:
∑mi(υxi2 υyi2 υzi2)2 V=Const;{displaystyle sum {frac {m_{i}(upsilon _{xi}^{2} upsilon _{yi}^{2} upsilon _{zi}^{2})}{2}} V=operatorname {Const} ;}
здесь mi{displaystyle m_{i}} обозначает массу i-й материальной точки, входящей в систему; υxi,υyi,υzi{displaystyle upsilon _{xi},upsilon _{yi},upsilon _{zi}} — составляющие ее скорости но осям x{displaystyle x}, y{displaystyle y}, z{displaystyle z}; V{displaystyle V} — потенциальная энергия системы.
2. Интегралы сохранения движения центра тяжести:
∑mi,υxi=Const,{displaystyle sum m_{i},upsilon _{xi}=operatorname {Const} ,}∑mi,υyi=Const,{displaystyle sum m_{i},upsilon _{yi}=operatorname {Const} ,}∑mi,υzi=Const.{displaystyle sum m_{i},upsilon _{zi}=operatorname {Const} .}
3. Интегралы сохранения момента количества движения:
∑mi(υixy−υiyxi)=Const,{displaystyle sum m_{i}(upsilon _{ix}y-upsilon _{iy}x_{i})=operatorname {Const} ,}∑mi(υiyz−υixyi)=Const,{displaystyle sum m_{i}(upsilon _{iy}z-upsilon _{ix}y_{i})=operatorname {Const} ,}∑mi(υizx−υixzi)=Const.{displaystyle sum m_{i}(upsilon _{iz}x-upsilon _{ix}z_{i})=operatorname {Const} .}
Здесь xi,yi,zi{displaystyle x_{i},y_{i},z_{i}} — координаты i-й материальной точки.
Для одной материальной точки, движущейся в поле центральной силы (т. е. силы, направленной к одному центру), момент количества движения также сохраняется. — Интеграл момента количества движения называют также и интегралом площадей. При его сохранении траекторией точки будет плоская кривая, и радиус-вектор движущейся точки будет описывать площадь, пропорциональную времени. В полярных координатах интеграл площадей (для одной точки) представляется в форме r2dφdt{displaystyle r^{2}{frac {dvarphi }{dt}}} (r{displaystyle r} — радиус-вектор, dφdt{displaystyle {frac {dvarphi }{dt}}} — угловая скорость). Интеграл площадей имеет существенное значение в теории движения планет.
Знание И. у. д. облегчает задачу исследования движения; так, если состояние системы определяется n{displaystyle n} величинами и известно m{displaystyle m} интегралов, то нам достаточно определить только (n−m{displaystyle n-m}) неизвестных, остальные неизвестные можно определить из интегралов. И. у. д. могут, конечно, иметь место не только для чисто механических систем.
Лит.: Уиттекер Е. Т., Аналитическая динамика, пер. с англ. И. Г. Малкина, М. — Л., 1937.
Определенный интеграл, формула ньютона – лейбница
Фигура, изображённая на рисунке 2, называется криволинейной трапецией. Криволинейная трапеция – фигура, ограниченная сверху графиком функции 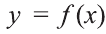 а; b], а по бокам -отрезками прямых х = а, х = b. Отрезок[а; b] называется основанием криволинейной трапеции.
а; b], а по бокам -отрезками прямых х = а, х = b. Отрезок[а; b] называется основанием криволинейной трапеции.
Возникает вопрос: «Как вычислить площадь криволинейной трапеции?»
Обозначим эту площадь через S. Оказывается, площадь S можно вычислить, опираясь на первообразную для функции f(х). Приведём соответствующие рассуждения.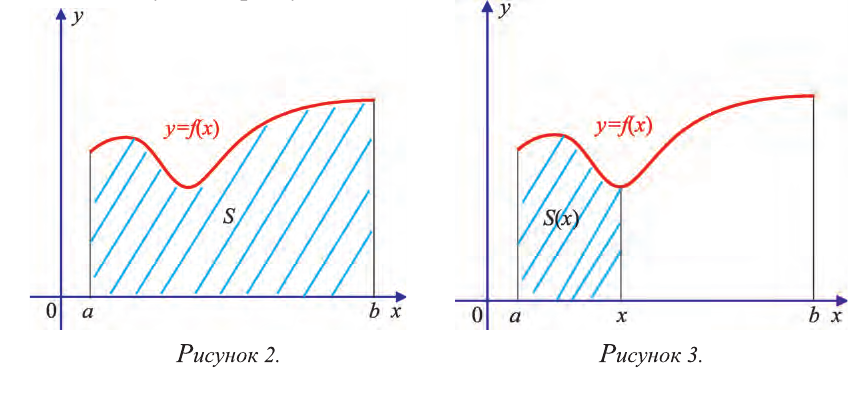
Обозначим площадь криволинейной трапеции с основанием [a; х] через S (х) (рисунок 3). Точка х – произвольная точка из отрезка [a; b]. В случае х = а отрезок [а; х] превращается в точку, поэтому S(a)=0; а при х = bS(b) = S.
Покажем, что функция S(х) является первообразной для функции f(х), то есть 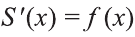
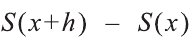 h > 0 (случай h < 0 рассматривается аналогично). Эта разность равна площади криволинейной трапеции с основанием [х; x h] (рисунок 4). Отмeтим, что при достаточно малых h эта площадь приблизительно равна
h > 0 (случай h < 0 рассматривается аналогично). Эта разность равна площади криволинейной трапеции с основанием [х; x h] (рисунок 4). Отмeтим, что при достаточно малых h эта площадь приблизительно равна 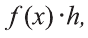
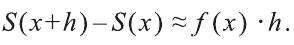
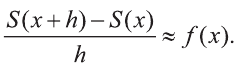
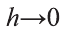 S'(х). Поэтому при
S'(х). Поэтому при 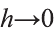
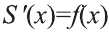 S(x) является первообразной для функции
S(x) является первообразной для функции 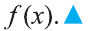 S(x) отличается от произвольной первообразной F(x) па постоянную величину, то есть
S(x) отличается от произвольной первообразной F(x) па постоянную величину, то есть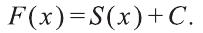 х=а получим
х=а получим 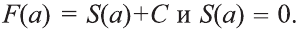
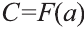
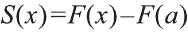 х=b, получим
х=b, получим 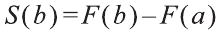
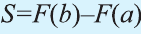
где F(x) – любая первообразная для функции f (х).
Таким образом, вычисление площади криволинейной трапеции сводится к нахождению первообразной функции F(x) для функции f(х), то есть к интегрированию функции f(х).
Разность F(b) – F(a) называется определённым интегралом от функции f(х) на отрезке [а; b] и обозначается так: 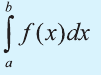 а до б от эф икс де икс»).Таким образом,
а до б от эф икс де икс»).Таким образом, 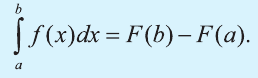
Формула (3) называется формулой Ньютона-Лейбница. Из (2) и (3) имеем:
Обычно при вычислении определенного интеграла принято обозначение:
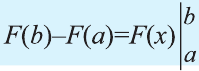
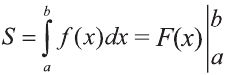
Приведём дополнительные сведения.
Задачу нахождения криволинейной фигуры свели к вычислению определённого интеграла. Рассмотрим непрерывную функцию, определённую на отрезке [а; b]. Разобьем этот отрезок точками а=х0, х1.., х1-n ,хn= b на равные отрезки 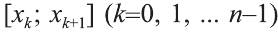
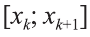
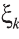
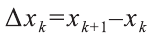
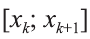
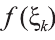 f(х) в точке
f(х) в точке 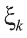
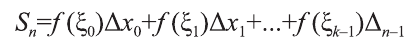
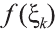 Sn. Тогда сумма S приближенно равна площади криволинейной трапеции
Sn. Тогда сумма S приближенно равна площади криволинейной трапеции 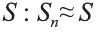 интегральной суммой функции f(х) по отрезку [а; b]. Пусть при стремлении n к бесконечности
интегральной суммой функции f(х) по отрезку [а; b]. Пусть при стремлении n к бесконечности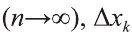 Sn стремится к некоторому числу. Вот это число называется определенным интегралом от функции f (х) на отрезке [а; b].
Sn стремится к некоторому числу. Вот это число называется определенным интегралом от функции f (х) на отрезке [а; b].
Пример:
Найдите площадь криволинейной трапеции, изображённой на рисунке 6.
Решение:
Согласно формуле (4) 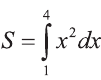
формуле Ньютона – Лейбиица (3). Очевидно, что функция
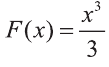
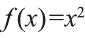
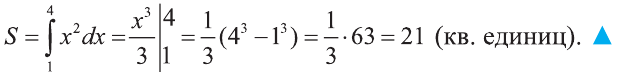 S = 21 (кв. единиц).
S = 21 (кв. единиц).
Пример:
Найдите площадь заштрихованной фигуры на рисунке 7.
Решение:
По формуле Ньютона-Лейбница и формуле (5): 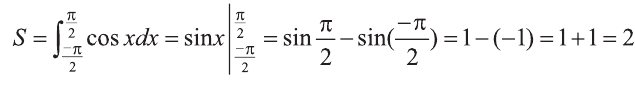

Пример:
Вычислить определённый интеграл 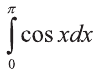
Решение:
По формуле Ньютона-Лейбница и формуле (5):
Ответ: 0. 
Пример:
Вычислить определённый интеграл 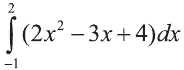
Решение:
По формуле Ньютона-Лейбница и формуле (5):
Ответ: 13,5. 
Пример:
Вычислить определенный интеграл 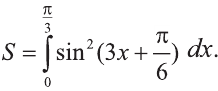
Решение:
Сначала найдём неопределенный интеграл: 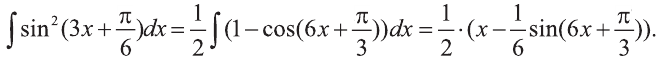
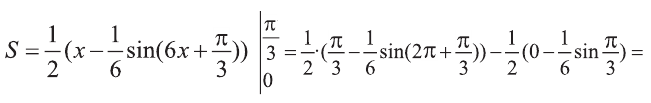
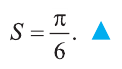
Пример:
Вычислить определённый интеграл 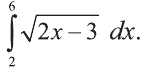
Решение:
Сначала найдем неопределенный интеграл:
Согласно таблице интегралов 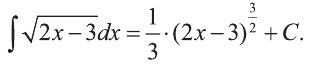
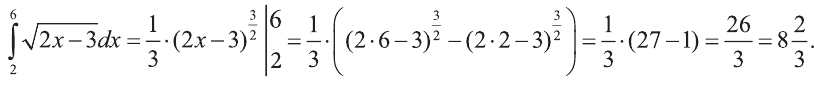
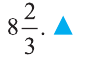
Определённый интеграл обладает следующими свойствами:
1.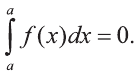
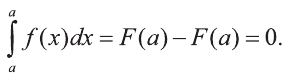
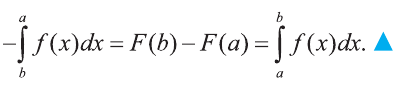
3.Пусть а, b, с – действительные числа. Тогда
(свойство аддитивности определённого интеграла).
4.Пусть 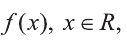
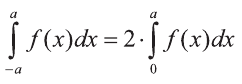 5.Если
5.Если 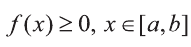
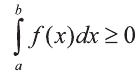 6.Если
6.Если 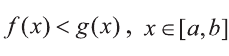
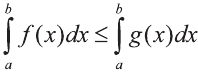
——
Первообразная
Вы умеете по заданной функции находить ее производную, знаете, что производная применяется во многих областях. В частности, умея дифференцировать, по данному закону 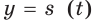
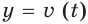
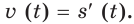
Нередко в механике приходится решать обратную задачу: находить закон движения по известному закону изменения скорости.
Например, из курса физики вам известен такой факт: если скорость изменяется по закону и 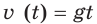
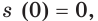
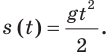
Вы знаете, что нахождение производной заданной функции называют дифференцированием. Обратную операцию, то есть нахождение функции по ее производной, называют интегрированием.
Определение. Функцию 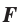 называют первообразной функцией (или коротко первообразной) функции
называют первообразной функцией (или коротко первообразной) функции 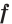 на промежутке
на промежутке 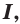 если для всех
если для всех 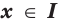 выполняется равенство
выполняется равенство 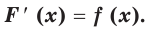 Например, функция
Например, функция 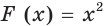
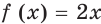
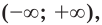
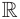
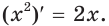
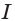
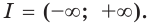
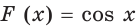
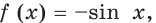
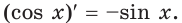
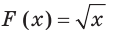
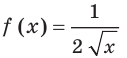
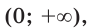
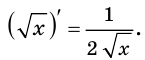
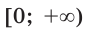
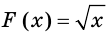
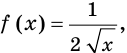
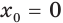
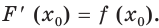
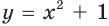
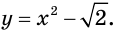
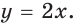
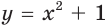
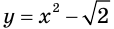
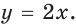
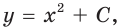
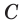
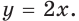
Цель интегрирования состоит в том, чтобы для заданной функции найти все ее первообразные на заданном промежутке.
Как связаны между собой все первообразные данной функции, указывает следующая теорема.
Теорема 24.1 (основное свойство первообразной). Если функция 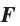 является первообразной функции
является первообразной функции 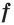 на промежутке
на промежутке 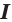 и
и  любое число, то функция
любое число, то функция 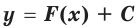 также является первообразной функции
также является первообразной функции 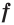 на промежутке
на промежутке 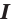 . Любую первообразную функции
. Любую первообразную функции 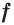 на промежутке
на промежутке 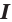 можно представить в виде
можно представить в виде 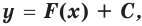 , где
, где 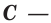 некоторое число.Доказательство. Поскольку функция
некоторое число.Доказательство. Поскольку функция 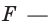
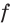
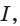
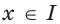
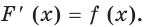
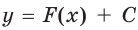
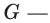
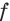
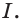
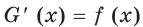
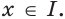
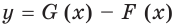
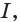
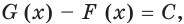
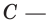
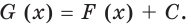
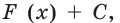
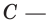 общим видом первообразных функции
общим видом первообразных функции 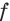
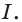
Из основного свойства первообразной следует, что графики любых двух первообразных данной функции можно получить друг из друга параллельным переносом вдоль оси координат (рис. 24.1).
Совокупность всех первообразных функции 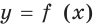
 неопределенным интегралом и обозначают
неопределенным интегралом и обозначают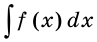
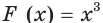
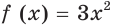
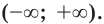
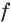
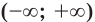
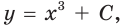
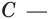
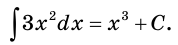
При решении задач на первообразную удобно пользоваться таблицей, приведенной на форзаце 3.
Покажем на примерах, с помощью каких соображений можно обосновать утверждения, приведенные в этой таблице.
Пример:
Найдите общий вид первообразных функции 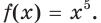
Решение:
Поскольку 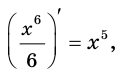
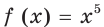
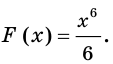
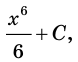
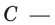
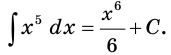
Пример:
Найдите общий вид первообразных функции 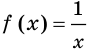
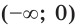
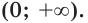
Решение:
На промежутке 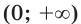
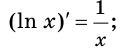
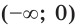
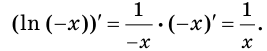
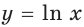
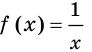
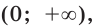
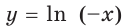
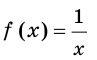
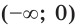
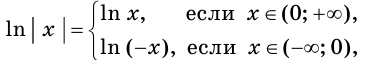
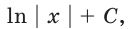
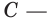
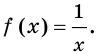
Пример:
Для функции 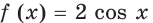
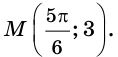
Решение:
Поскольку 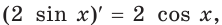
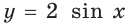
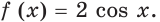
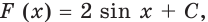
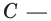
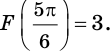
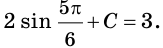
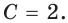
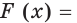
Замечание.
Можно доказать, что функция 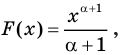
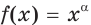
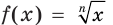
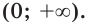
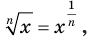
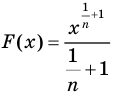
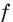
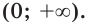
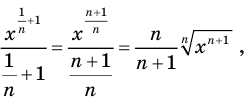
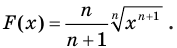
Поверхностный интеграл второго рода
Пусть в 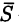
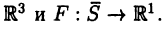
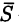
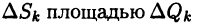

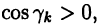
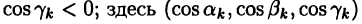
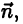
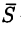
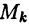 Поверхностным интегралом 2-го рода от функции F(х,у,z) по выбранной стороне поверхности
Поверхностным интегралом 2-го рода от функции F(х,у,z) по выбранной стороне поверхности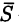
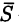
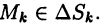
В общем виде поверхностный интеграл 2-го рода записывают так
Для существования (45.2) достаточно потребовать, чтобы 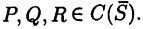
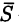
Физический смысл поверхностного интеграла 2-го рода будет рассмотрен в следующей главе. Здесь же приведем формулу для его вычисления.
Пусть уравнение поверхности 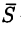
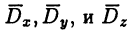
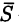
Пример:
Вычислить
где 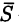
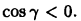
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Правила нахождения первообразной
При нахождении производных функций вы пользовались не только формулами, записанными в таблице (см. форзац 2), но и правилами дифференцирования. В этом пункте мы рассмотрим три правила нахождения первообразных.
Теорема 25.1. Если функции 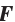 и
и 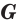 являются соответственно первообразными функций
являются соответственно первообразными функций 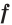 и
и 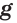 на промежутке
на промежутке 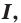 то на этом промежутке функция
то на этом промежутке функция 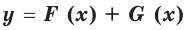 является первообразной функции
является первообразной функции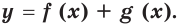
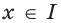
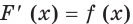
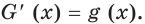
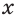
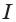
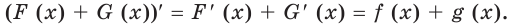
Из теоремы 25.1 следует, что
где 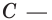
Аналогично можно доказать, что
Теорема 25.2. Если функция 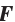 является первообразной функции
является первообразной функции 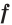 на промежутке
на промежутке 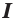 и
и  некоторое число, то на этом промежутке функция
некоторое число, то на этом промежутке функция 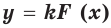 является первообразной функции
является первообразной функции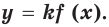
Докажите теорему 25.2 самостоятельно.
Теперь можно записать: 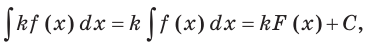
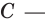 Теорема 25.3. Если функция
Теорема 25.3. Если функция 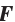 является первообразной функции
является первообразной функции 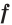 на промежутке
на промежутке 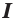 и
и  некоторое число, отличное от нуля, то на соответствующем промежутке функция
некоторое число, отличное от нуля, то на соответствующем промежутке функция 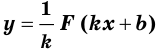 является первообразной функции
является первообразной функции 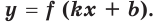
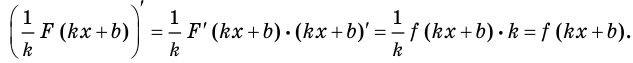
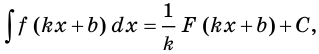
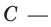
Пример:
Найдите общий вид первообразных функции 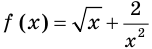
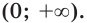
Решение:
Напомним, что функция 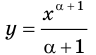
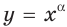
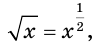
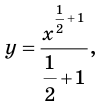
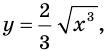
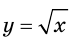
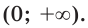
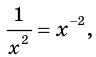
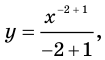
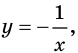
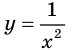
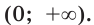
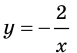
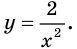
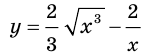
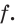
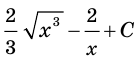
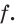
Решение примера 1 можно записать и так:
Пример:
Найдите одну из первообразных функции:
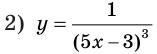
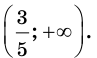
Решение:
1) Поскольку функция 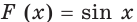
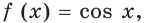
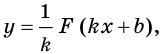
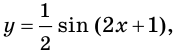
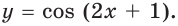
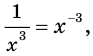
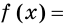
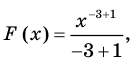
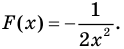
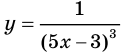
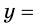
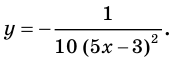
Пример:
Для функции 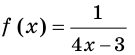
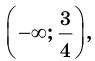
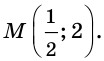
Решение:
Согласно теореме 25.3 запись 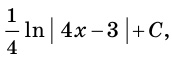
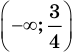
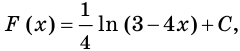
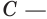
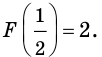
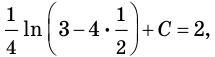
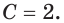
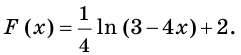
Пример:
Скорость движения материальной точки по координатной прямой изменяется по закону 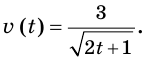
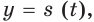
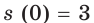
Решение:
Функция 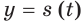
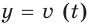
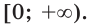
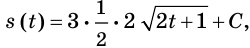
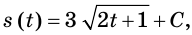
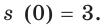
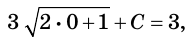
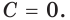
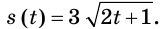
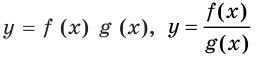
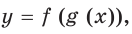
Таблица интегралов
Опираясь на таблицу производных можно составить таблицу интегралов.
Для того, чтобы функция F(x) была первообразной для функции f(х) на некотором промежутке X, необходимо, чтобы обе функции F(x) и f(х) были определены на этом промежутке X.
Например, 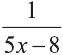
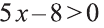 х > 1,6, согласно таблице интегралов, первообразная равна —
х > 1,6, согласно таблице интегралов, первообразная равна — 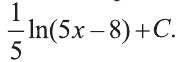
Используя правила дифференцирования, можно сформулировать некоторые правила интегрирования.
Пусть функции F(x) и G(x) на некотором промежутке являются первообразными для функций 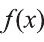
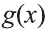 Правило 1: Функция
Правило 1: Функция 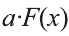
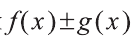
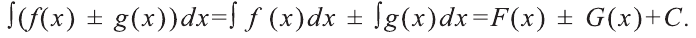 Правило 2: Функция
Правило 2: Функция 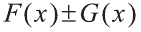
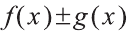
Пример:
Проинтегрируйте функцию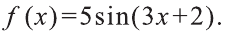
Решение:
Согласно правилу 1 и 9 пункту таблицы интегралов: 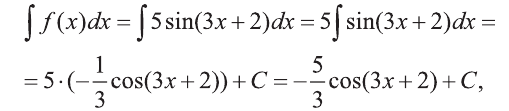
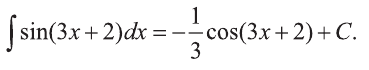
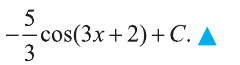
Пример:
Проинтегрируйте функцию 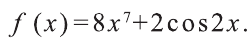
Решение:
Найдём интеграл этой функции, используя правила 1, 2 интегирования, а также пункты 1 и 10 таблицы интегралов: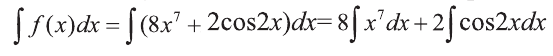
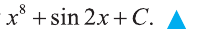
Пример:
Вычислить интеграл 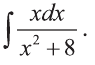
Решение:
При решении таких примеров удобно использовать замену переменных.
Именно, обозначим х2 8 = u тогда,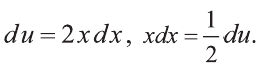
Проверка: Найдём производную от полученной функции и получим
подынтегральную функцию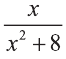
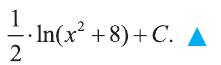
Пример:
Вычислить интеграл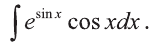
Решение:
Сделаем замену sinx = t. Тогда 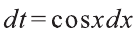
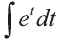
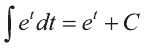
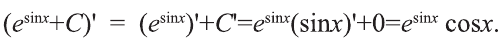
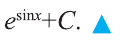
Пример:
Вычислить интеграл 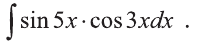
Решение:
При вычислении этого интеграла помогает тождество 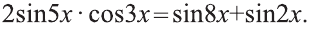
Тогда
Ответ: 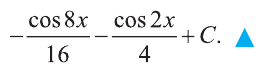
Пример:
Вычислить интеграл 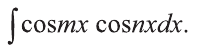
Решение:
Согласно тождеству 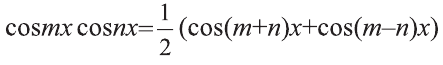
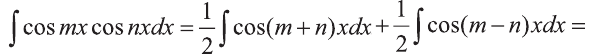
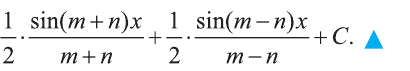
Пример:
Вычислить интеграл 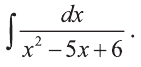
Решение:
Для подынтегральной функции справедлива равенства: 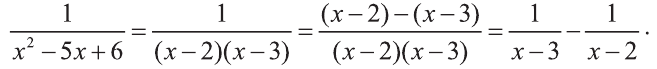
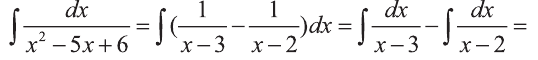
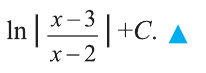
Пример:
Вычислить интеграл 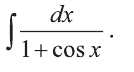
Решение:
Для вычисления этого интеграла воспользуемся 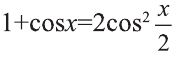
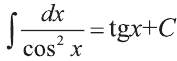
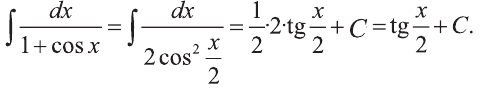
Проверка:
Ответ: 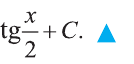
Пример:
Вычислить интеграл 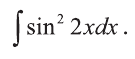
Решение:
Для вычисления этого интеграла воспользуемся 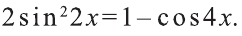
Приведём также правило интегрирования по частям.
Правило 3*.
Если на некотором интервале X функции 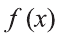
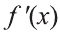
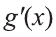
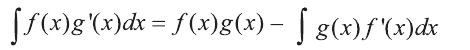
Эта формула называется формулой интегрирования по частям.
Доказательство формулы следует из правила дифференцирования произведения функций 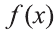
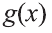
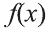
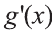 выражения
выражения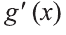
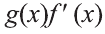
Пример:
Вычислить интеграл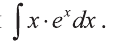
Решение:
Подберём 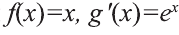
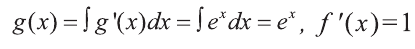
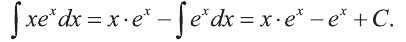
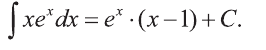
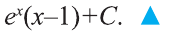
Пример:
Вычислить интеграл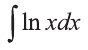
Решение:
Представим подынтегральную функцию 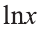
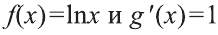
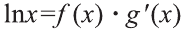
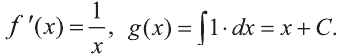
Согласно формуле (1),
Значит, 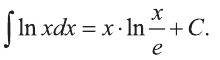
Проверка:
Ответ: 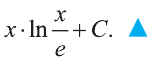
Пример 3.
Для нахождения интеграла удобно положить 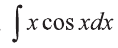
Решение:
В этом случае 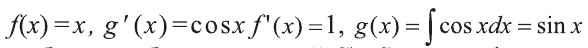 С). Согласно формуле интегрирования по частям,Ответ:
С). Согласно формуле интегрирования по частям,Ответ: