Новая книга с примерами в SimInTech

2 основные положения модели

В литературе и сети приведено довольно много моделей квадрокоптеров, есть некоторые модели гекса- и октокоптеров. Однако, изложенного в системном и методичном виде со всеми подробностями — практически ничего нет (по крайней мере, в русскоязычном сегменте, из тех материалов что удалось найти). Наиболее методично теоретический подход к моделированию мультироторного БПЛА изложен в работах [1] и [2].

Опуская некоторые выкладки, изложенные в этих работах (они легко гуглятся), можно выделить следующие допущения и упрощения, принятые в модели:

1. Двигатель моделируется как инерционное звено (апериодическое звено) первого порядка, на вход которому подается заданное значение угловой скорости, а на выходе – текущее (измеренное) значение угловой скорости вращения. Интегрируя скорость вращения, можно получить и текущий угол поворота если это зачем-то нужно. Силу тяги ВМГ развивает пропорциональную квадрату угловой скорости (равно как и реактивный момент каждого двигателя, но в нашем случае он будет 0), а именно:

   

   где, для выбранной винтомоторной группы (согласно её характеристике):
   ,
   — реактивный момент двигателя,
   – текущая угловая скорость, рад/с.

2. Мультироторный аппарат моделируется как твёрдое тело и представляет собой жёсткую (недеформируемую) раму постоянной массы, симметричную по трём главным осям, с прикрепленными к ней ВМГ в одной плоскости, в которой находится и центр масс аппарата. При этом ВМГ расположены на восьми лучах (4 из них одной длины, а другие 4 могут быть другой длины) и жестко закреплены относительно рамы. Таким образом можно говорить о том, что радиус-векторы центров ВМГ и орты силы тяги каждой ВМГ – суть геометрические константы в системе координат, связанной с коптером. Другими словами, величина [Н], вычисленная в модели ВМГ, является модулем вектора силы, приложенного всегда в определенном направлении и в определенной точке коптера. В процессе полета это направление будет меняться, конечно, но относительно рамы коптера (и связанной с ней системы координат) оно остаётся неизменным.
3. Используется две системы координат: а) неподвижная инерциальная, связанная с Землёй и б) подвижная, связанная с коптером. Системы координат обозначим буквами I и B (от английских слов inertial – инерциальный и body – тело). При этом оси систем направлены: -вправо, -на наблюдателя, -вниз, — вправо вдоль луча первой ВМГ, -на наблюдателя вдоль луча третьей ВМГ, -сверху вниз при нормальной ориентации коптера (см. рисунок):
   
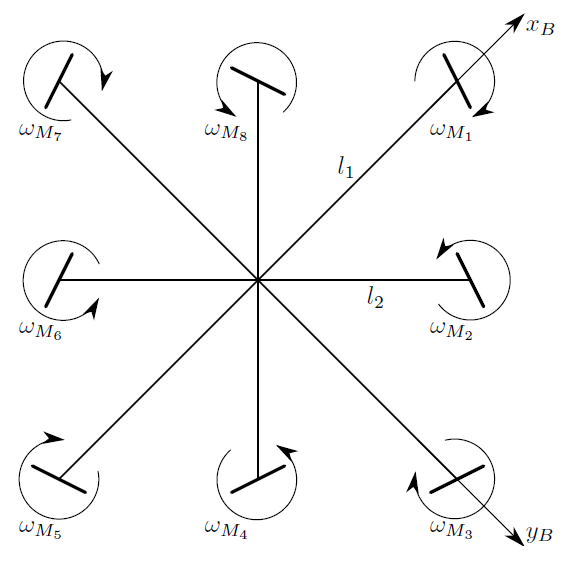
   Тогда, в системе координат B векторы центров ВМГ будут равны:

   

   где – длина луча у 1, 3, 4 и 5-й ВМГ, а – длина лучей у 2, 4, 6 и 8-й ВМГ.

   Для того чтобы коптер управлялся (хотя бы немного) по курсу, в нашем случае отсутствия реактивного момента двигателей, вектора сил тяги каждой ВМГ должны быть немного отклонены от вертикального направления (повёрнуты вокруг каждого луча на небольшой угол порядка 1…5 градусов, причем в разные стороны – четные в одну а нечетные в другую). Если обозначить этот угол как , орты можно получить в следующем виде:

   

   На основе этих геометрических констант (напомним, они являются константами только в системе координат B, связанной с коптером) строится весь дальнейший каркас модели, поэтому они важны. В общем случае, винтомоторных групп может быть другое количество и направлены они могут быть в других направлениях, и располагаться у коптера в других местах.
   О применяемых системах координат подробно изложено в [1].

4. Силы, которые будут учтены в модели. На коптер действуют:
   4.1) Сила тяжести. Направлена всегда вниз вдоль оси инерциальной системы координат . Сила тяжести – постоянная величина, зависит только от массы коптера. Масса коптера принимается постоянной и не меняется (хотя в процессе моделирования её можно будет менять, имитируя дополнительный полезный груз, навешенный на коптер).
   4.2) Силы тяги ВМГ – их всего 8, они направлены вдоль своих направлений, модуль сил вычисляется в зависимости от угловой скорости вращения соответствующей ВМГ.
   4.3) Сила сопротивления воздуха (и/или ветер) – моделируется как состоящая из двух компонент. Сила сопротивления воздуха прямо пропорциональна плотности воздуха, квадрату линейной скорости объекта в воздухе и характерной площади сечения в выбранном направлении (коэффициент формы). Сила ветра – внешняя возмущающая сила, задается произвольным образом или при помощи дополнительной «модели ветра» (в настоящей статье не рассматривается).
   4.4) Внешняя сила или возмущение – произвольное внешнее воздействие. В модели такая возможность заложена как простой способ в дальнейшем проверять на устойчивость регуляторы по каждому из направлений.
5. Моменты, учитываемые в модели:
   5.1) Реактивный момент двигателей ВМГ. В нашей модели он равен нулю, из-за парности двигателей и винтов в каждой ВМГ в общем случае – следует учитывать. В некоторых аппаратах этот момент используется и для управления по курсу.
   5.2) Явление прецессии – в рассматриваемой модели он нулевой, в общем случае его нужно считать.
   5.3) Момент сопротивления воздуха – аналогично силе сопротивления воздуха, прямо пропорционален плотности воздуха, квадрату угловой скорости коптера и коэффициенту формы.
   5.4) Опрокидывающий момент от ветровой нагрузки.
   5.5) Внешний возмущающий момент – для отладки регуляторов.
   5.6) Моменты от сил тяги ВМГ. Поскольку винты расположены не в центре масс коптера, каждый из них будет создавать свой поворотный момент. Это, пожалуй, основной фактор, который управляет ориентацией коптера в пространстве.

(pdf) modeling and position control of tethered octocopters

3 нелинейные уравнения динамики октокоптера

С учетом принятых допущений, и того что коптер моделируется как единое твёрдое тело, основа модели динамики коптера очень проста – это второй закон Ньютона, который в векторной форме выглядит следующим образом, всего два простых уравнения:

где

– импульс коптера, а

– момент импульса коптера,

– его масса,

– тензор инерции (линейный оператор момента инерции).

суть суммы всех сил и всех моментов, действующих на коптер.

Легко видеть, что всё было бы очень просто и очевидно, если бы правые части были небольшими, а тензор инерции не зависел бы от ориентации коптера (как если бы коптер был шаром). Но из-за вращения коптера, а также из-за обилия сил и моментов, конечные уравнения, записанные в инерциальной системе координат, получатся очень громоздкими, даже без учета прецессии и реактивных моментов ВМГ.

Поэтому используется следующий математический приём – уравнения, записанные в инерциальной системе координат, переводятся в систему координат B, связанную с коптером, в которой слагаемые правой части (их запись) получается гораздо более лаконичной и удобной. Подробнее этот приём описан в [1], приведём здесь лишь основные соотношения.

Подставив в приведенные уравнения второго закона Ньютона значения для импульса и момента импульса коптера, для инерциальной системы координат получим:

В этих уравнениях математически очень сложны правые части, а уравнения динамики в связанной системе координат

B

(где правые части более просты) – не могут быть получены так легко, поскольку система координат, связанная с коптером – вращается.

В математике есть два основных подхода к преобразованию векторов из одной системы координат в другую и обратно – матрицы поворота и кватернионы. Последние более универсальны, первые – проще. В настоящей модели используются матрицы поворота. Если ориентацию коптера представить тремя углами: крена φ (roll), тангажа θ (pitch) и рыскания/курса ψ (yaw), а матрицы преобразования из системы I в B и обратно обозначить как и , то любой вектор записанный для системы координат I, можно перевести в систему координат B, и наоборот, используя умножение соответствующей матрицы на вектор, например: , или . Чтобы лучше понимать написанное далее, прокомментируем ещё раз как понимать матрицы поворота и вектора в пространстве: система координат I неподвижна, относительно неё летает и вращается коптер, а вместе с ним и связанная система координат B. Просуммировав все силы, которые действуют на коптер, можно получить вектор (аналогично и с моментом сил), и в каждый момент времени он является вектором с вполне определенной длиной и направлением в пространстве. Но раскладывая его на проекции по осям – в разных системах координат мы получим разные величины проекций. Всё что делает матрица поворота – это переводит одни проекции вектора в другие, при этом сам вектор никуда не поворачивается и не изменяет своей длины, в выбранный момент времени. Если проекции сравнить с тенями вектора, то матрицы поворота преобразуют одни тени в другие, всё. Больше они ничего не делают и сложностей кроме вычислительных не представляют.Нам они нужны только из-за того, что вычислять и суммировать силы и моменты сил, действующие на коптер, гораздо проще в связанной системе координат B. В ней же проще провести численное интегрирование уравнений, чтобы получить величины угловой и линейной скоростей коптера и , а потом обратной матрицей поворота вычислить (вычислить алгебраически – матрицы поворота это простые уравнения) эти же скорости для инерциальной системы координат I и там уже, интегрируя дальше, вычислить линейные и угловые координаты коптера.

Приведем используемое выражение для матрицы поворота из системы I в B, записав для краткости функции косинуса и синуса как cos() = c() и sin() = s():

Отметим еще раз, что в каждый момент времени эта матрица, очевидно, будет получаться разной т.к. меняются углы ориентации коптера. Но это просто алгебраические вычисления, без никаких дифференциальных уравнений. Сама матрица — не константа, и у неё есть производная по времени.

Реализованная методом структурного моделирования, матрица в среде SimInTech выглядит как показано на рисунке 1.

Рисунок 1. Матрица поворота из системы I в систему координат B

Тогда, для вектора линейной скорости можно записать:

а для момента импульса

Опуская промежуточные выкладки (в том числе производную матрицы поворота, которая получается равной в итоге векторному произведению угловой скорости объекта на саму матрицу поворота, взятое с обратным знаком), для первого из рассматриваемых уравнений динамики получим следующее выражение в связанной с коптером системе координат

B

а для второго уравнения, учитывая что

и так как во вращающейся связанной системе координат тензор инерции константа и его производная по времени равна нулю, а

получим:

Итого, запись II закона Ньютона для вращающейся системы B, по сравнению с исходными уравнениями, дополнилась двумя векторными произведениями.

Переменными состояния коптера в такой записи являются две векторных величины (или 6 скалярных) – вектор линейной скорости и вектор угловой скорости. Алгебраически это будет 6 переменных – три проекции линейной скорости и три проекции угловой скорости.

Получив значения скоростей коптера (сначала в системе B), их можно матрицей обратного поворота преобразовать к системе I, еще раз проинтегрировать и получить уже значения координат и, следовательно, положение объекта в пространстве, в инерциальной системе координат.

Единственное что мы еще не сделали по уравнениям – не записали выражения для сил и моментов, действующих на коптер. Сделаем это ниже, в системе координат B. Согласно допущениям, учитываем и обозначим индексами: M — работу двигателей, только в части создаваемой силы тяги и моментов от неё, D — силу сопротивления воздуха (вместе с ветром)

https://www.youtube.com/watch?v=5UV25lRslOY

Сила тяжести в связанной системе координат будет «поворачиваться» в зависимости от ориентации коптера.

Распишем подробнее чему равны слагаемые:

Здесь уже фигурируют угловые скорости вращения ВМГ, а не коптера. Напомним, что орты сил тяги у нас записаны для системы координат

B

и там являются константами – очевидно, что их можно вычислить 1 раз, общий коэффициент вынести здесь за скобку и сильно упростить вычисления. Если бы мы записывали уравнения динамики в системе

I

, то данное выражение обросло бы ещё 8-ю умножениями на матрицу поворота каждого орта и это пришлось бы считать на каждом шаге расчета.

Сила сопротивления воздуха (при отсутствии ветра):

Внешнее возмущение – нулевое, по желанию пользователя, он может сам установить то или иное значение позже, до расчета, или в процессе моделирования.

Момент сил тяги двигателей запишем как:

Момент сопротивления воздуха (подробнее см. [1]):

Ещё раз отметим, что расчет прецессии и реактивных моментов ВМГ в данной статье для краткости изложения опущен.

Чтобы не ошибиться при переходе от векторных уравнений к скалярным, записанным по осям, проще воспользоваться пакетом типа MathCAD или Maple, в котором большинство преобразований можно выполнить автоматизированно, в символьном виде и получить требуемые 6 уравнений динамики, записанные по осям подвижной системы координат B.

В наиболее компактной форме полученные и решаемые уравнения динамики выглядят так:

Интегрируя их и получив значения скоростей в системе В, можно посчитать скорость и углы ориентации в инерциальной системе координат I:

Про матрицу преобразования из угловой скорости коптера в скорости поворота по углам Эйлера

подробнее см. в [1].

1 Решение дифференциальных уравнений методом структурного моделирования

Для решения дифференциального уравнения методом структурного моделирования используются либо типовые звенья первого и второго порядков – если дифференциальное уравнение линейно и подходит под один из типов, либо используется блок типа «Интегратор», на вход которому подаётся правая часть уравнения, а на выходе будет искомая интегральная величина. Приведём пример – заготовку для решения нашей системы из 6-ти дифференциальных уравнений, см. рисунок 2.

На рисунке 2 представлена «основа» динамической части модели октокоптера, которую формируют 6 3 3 блоков типа «интегратор». Первые шесть блоков, получая на вход правые части дифференциальных уравнений (вычислим их ниже) – ускорения коптера по осям , – занимаются интегрированием и вычислением скоростей коптера по этим же осям (тоже, в связанной с коптером системе В).

Следующие три интегратора принимают линейные скорости в системе координат I (полученные алгебраически из скоростей в системе B путём применения матрицы поворота) и, интегрируя их, получают координаты центра масс коптера в инерциальной системе координат

И, еще три блока типа «интегратор» занимаются вычислением углов ориентации коптера, интегрируя их производные (угловые скорости) в системе I, полученные из угловых скоростей коптера в системе B применением матрицы . Здесь же реализовано и вычисление нужных тригонометрических функций от углов поворота.Рисунок 2. Структура модели октокоптера

Обилие блоков «в память» и «из памяти» обусловлено многократным использованием в других частях модели полученных величин – например, по рисунку 1 видно что тригонометрические функции от углов ориентации используются многократно и оптимально вычислить их в одном месте схемы а потом уже использовать по мере необходимости.

Если бы у нас была более простая ситуация – одно дифференциальное уравнение второго порядка (классический второй закон Ньютона a = F/m), например в проекции на ось x, то его решение таким же способом выглядело бы как на рисунке 3:

Рисунок 3. Двойное интегрирование

В случае коптера используется такой же приём, т.е. если на выходе из интегратора имеется какая-то величина, то слева от него – обязательно производная этой же величины. Таким образом записываются и решаются дифференциальные уравнения методом структурного моделирования, если не прибегать к встроенному языку программирования SimInTech (где зачастую удаётся сделать то же самое еще более просто, но менее очевидно).

В субмодели W(B->I) реализована матрица преобразования из угловой скорости в системе B в производные углов Эйлера, см. рисунок 4 и [1] для подробностей.

Рисунок 4. Матрица

2 Правые части уравнений модели коптера

Для замыкания модели необходимо посчитать и реализовать все правые части у шести основных уравнений, то есть спроецировать полученные в разделе 2 векторные уравнения на оси и результат нарисовать в схеме SimInTech. Опуская выкладки (их читатель может выполнить самостоятельно на листке бумаги, или при помощи какого-то символьного математического ПО), приведем окончательный вид уравнений. Из-за громоздкости, приводить будем по слагаемым в правых частях.Сила тяги винтомоторных групп

где

— сила тяги i-ой ВМГ в текущий момент времени.

Сила сопротивления воздуха при отсутствии ветра – формулы приведены выше, проекции будут равны:

$$display$$F_{Dx}(t) = 0.5 cdot rho cdot C_Dcdot A_{yz}cdot v_xcdot |v_x|,\ F_{Dу}(t) = 0.5 cdot rho cdot C_Dcdot A_{xz}cdot v_уcdot |v_у|,\ F_{Dz}(t) = 0.5 cdot rho cdot C_Dcdot A_{xy}cdot v_zcdot |v_z|.\$$display$$

Сила тяжести, в проекции на оси подвижной системы координат, слагаемое очевидно будет равно:

И последнее слагаемое в уравнении линейной скорости коптера – векторное произведение скоростей:

Если аккуратно подставить полученные проекции в уравнение для производной линейной скорости коптера, и дальше реализовать всё это в SimInTech, по осям, получим следующие структурные схемы, представленные на рисунках 5, 6 и 7 (показаны проекции только на ось , на другие оси результат аналогичен с точностью до слагаемых):Рисунок 5. Линейное ускорение коптера по оси . Рисунок 6. Сила тяги ВМГ по оси . Рисунок 7. Сила сопротивления воздуха по оси .

Итого, на данном этапе мы до конца реализовали одно из шести основных уравнений (согласно рисунку 2 – вычислили вход в первый интегратор). Остальные оборванные там входы для сил вычисляются аналогично. Рассмотрим уравнение для моментов и для вычисления угловой скорости, а точнее – его слагаемые в правой части:

Сумма моментов сил тяги всех ВМГ:

где

– сила тяги i-ой ВМГ в текущий момент времени,

-плечи сил (длины лучей рамы коптера для нечетных и четных ВМГ).

Момент сопротивления воздуха (при отсутствии ветра):

Векторное произведение угловой скорости на произведение тензора инерции и угловой скорости:

Итого, после подстановки этих слагаемых в дифференциальное уравнение для угловой скорости, и реализации полученного в среде SimInTech, получим следующие структурные схемы:

Рисунок 8. Угловое ускорение коптера вокруг оси . Рисунок 9. Момент сил тяг ВМГ вокруг оси . Рисунок 10. Сила сопротивления воздуха при вращении вокруг .

3 Система уравнений динамики октокоптера в структурном виде

Итого, если представить все реализованные уравнения рядом на схеме, получим следующую картину (рисунок 11). Как видно, она довольно громоздка, даже без включения сюда других дифференциальных уравнений для вычисления координат коптера и углов поворота.

А поскольку в дальнейшем на каждое уравнение будут навешиваться еще дополнительные сервисные вычисления (ускорений, различных составляющих сил и моментов, для отладки модели и регуляторов), целесообразнее эти уравнения структурно разделить на 6 субмоделей, что и было сделано, в каждой из которых решается своё уравнение, см. рисунок 12.

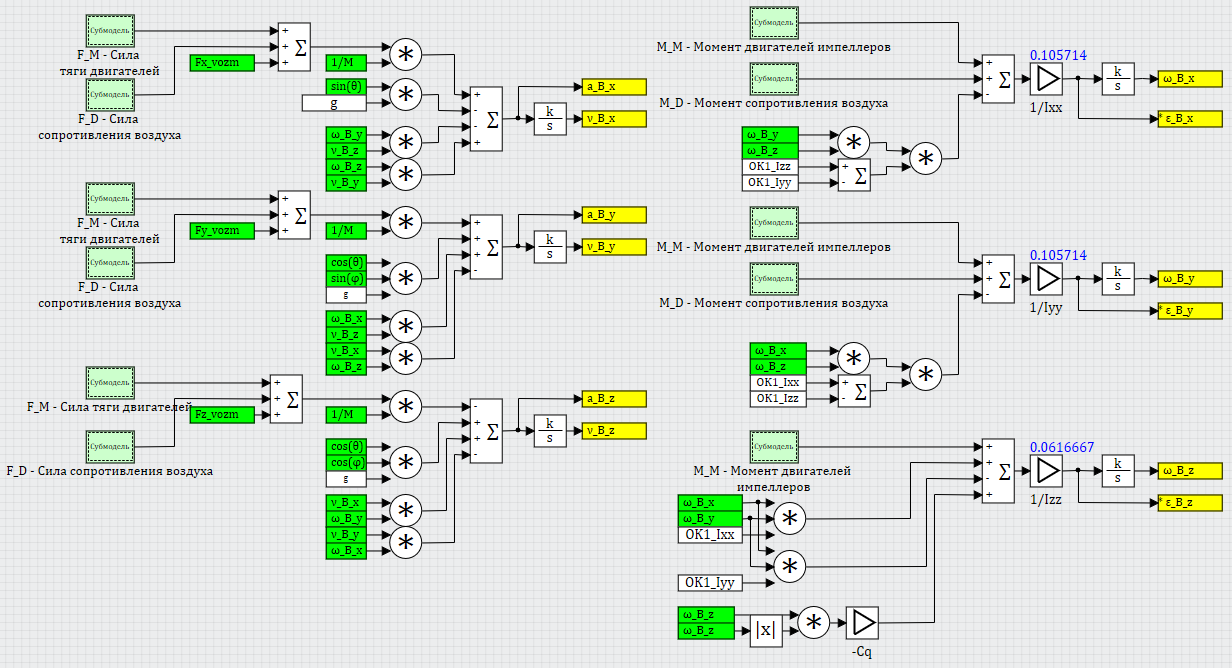Рисунок 11. Уравнения динамики коптера в связанной системе координат В. Рисунок 12. Модель динамики коптера, верхний уровень.

В принципе, все приведенные уравнений и структуры можно было реализовать и средствами языка программирования SimInTech, но тогда они были бы не так наглядны.

Входными величинами здесь являются силы тяги двигателей (они считаются вне этих уравнений, в зависимости от текущей скорости вращения каждой ВМГ и её силовой характеристики), внешняя возмущающая сила и момент сил (задаются пользователем произвольно) и сила тяжести.

Выходными величинами являются ускорения, скорости и положение (координаты) коптера – ускорения и скорости в системах координат B и I, положение – в системе I (положение коптера в системе B практической ценности почти не имеет т.к. сама система движется вместе с коптером и совпадает по положению с ним – то есть там положение коптера всегда будет нулевым).

В продолжении мы рассмотрим создание системы управления для октокоптера, а так же рассмотрим принципы создания видеокадров управления.

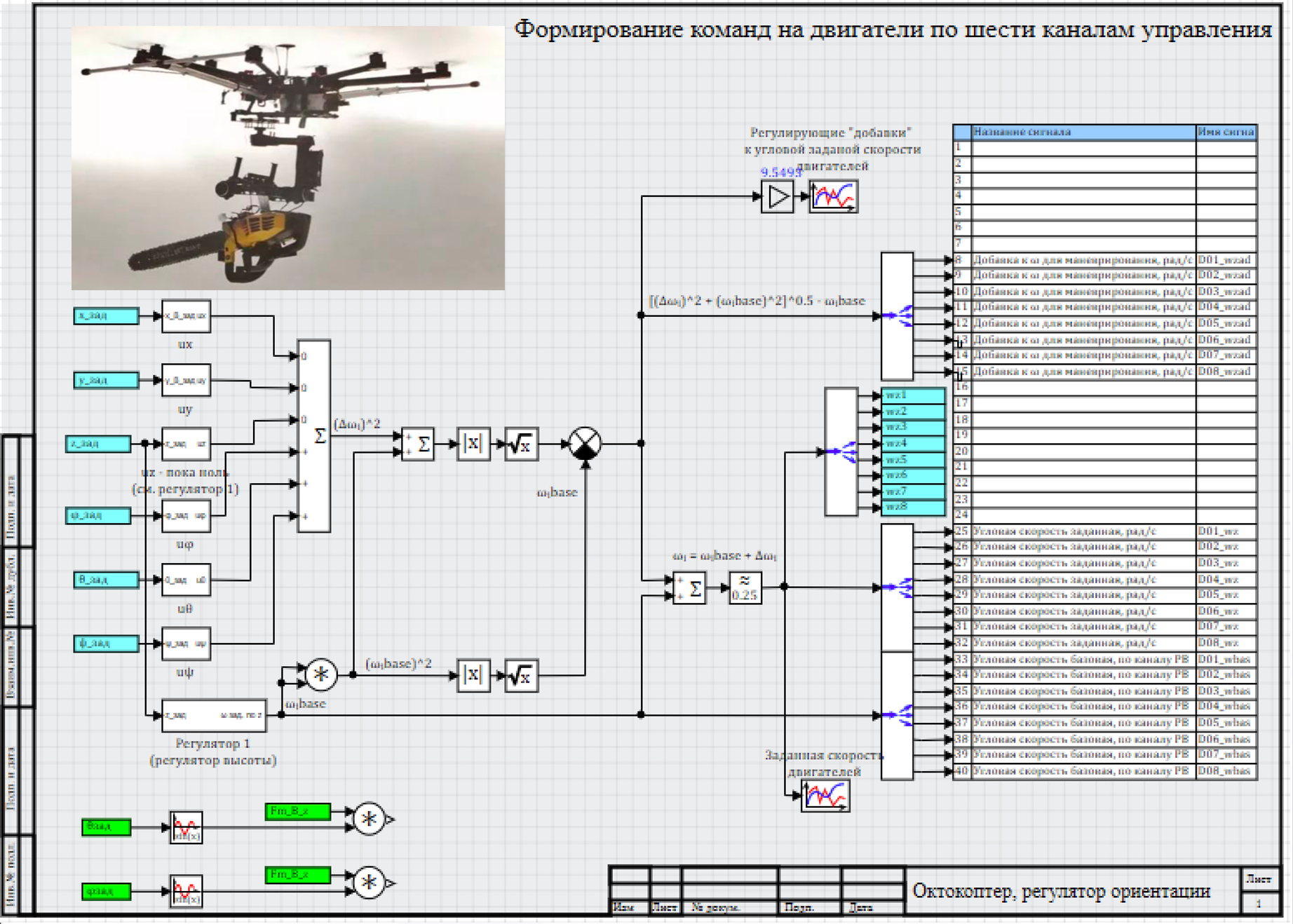
Модель коптера, рассмторенную в статье, можно взять по этой ссылке.

Как я октокоптер собирал.

Комплектующие рамы

• Как только вы соберетесь к постройке своими руками квадрокоптера вы получите хороший опыт в строительстве, но это уже не для новичков.
• Исключением являеся, если вы внимательно следуете инструкциям по сборке квадрокоптера.
• Об использованных методах постройки рам можно узнать из каждого “журнала постройки”.
• Есть достаточно интересные модели рам, которые не разрушаются, например спортивно-акрабатические рамы Hoverthings flip 380 sport frame.
• Эта рама использует жесткую и сильные карбоновые лучи которые обрабатываются на ЧПУ станке из толстоко стекловолокна.
• Это позволяет использовать те же моторы и регуляторы ESC, что и в раме F450 DJI c пропеллерами до 10 дюймов.
• Я купил Флип Sport Kit плюс дополнительная пара “вкладка” секций типа центр и дополнительных 7/8 “прокладками”.
• Рама позволяет размещать батарейку под основной платой специальными держателями.
• Так же использовать специальный регулятор 4-в-1 помещенному между центральными пластинами рамы.

• Совмещенный регулятор ESC 4 в 1 ESC производит меньше помех и компактен, чем 4 обычных регулятора ESC и плата распределения питания.
• Я использую карбоновые 10 дюймовые пропеллеры, потому что они очень жесткие и очень эффективные.
• Моя цель заключается в создании еще более жесткого и более высокопроизводительного квадрокоптера, чем DJI F450.
• Хотя это небольшой квадрокоптер является мощным и достаточно гибким, чтобы использовать FPV видео и / или камеру GoPro с “подвесом”.

• Рама Tarot 650 из карбона довольно большая и позволяет устанавливать пропеллеры до 17 дюймов.
• Я использую моторы 360kv медленной скорости и большого диаметра, которые предназначены для использования более эффективных и больших пропеллеров на низких скоростях.
• Я буду использовать разнообразные пропеллеры – от 14 до 17 дюймов, чтобы исследовать производительность и эффективность при различных размерах пропеллеров.
• Хотя акрабатический спортивный квадрокоптер 330, который показан выше может быть целесообразным для первого квадрокоптера этот Tarot 650, безусловно, нет.
• Это четырехмоторный аппарат достаточно велик, чтобы быть тяговитым и долгим в полете на выносливость и нести большую видео или фотокамеру, но:
• Для подъема полезной нагрузки в 2кг с квадрокоптером вам нужно уточнить конфигурацию моторов и пропеллеров.
• Четыре мотора Tigermotor MN4010 475KV стоимостью около $ 86 каждый, четыре 15 х 5 или 16 х 5 пропеллера и четыре высококачественных регулятора ESC 30А.
• Так же нужно 10000 мАч 4-х баночную Lipo батарейку (две 5000мАч) для достижения примерно 10 минут полетного времени на 4KG общего веса.
• Квадрокоптер способный поднять общую массу 4кг (включая 2кг полезной нагрузки) и уметь взлетать при 50% тяги (это необходимость по технике, а так же иметь возможность 6кг взлета).
• Вам понадобится 16х5 пропеллеры для достижения тяги и эффективности необходимые для подъема 4KG с разумным временем полета.
• Именно поэтому требутся большие двигатели с минимальным кВ, они должны быть высокого качества, что бы выдержать непрерывную высокую нагрузку производительности.
• Это настоятельно рекомендуется, что бы вы не пытались построить один из таких апаратов в качестве первого из непонятно чего.
• Есть очень полезная ссылка для расчета производительности различных мультикоптеров и их компонентов – калькулятор квадрокоптера: eCalc

Новая книга с примерами в simintech

Особенности включают в себя:

Высокоточная подержка удержания высоты позволит спокойно летать сразу.
Или выбререте удивительный режим “простой полет” (Simple mode), что делает ArduCopter одним из самых простых в управлении.
Не беспокойтесь за слежением орентации вашего квадрокоптера, пусть полетный контролер этим занимается сам!

Вам не потребуются знания в программировании. Просто используйте простую в использовании программу на
рабочем столе, что бы загрузить последнюю прошивку одним щелчком мыши и настройте с помощью
программного обеспечения Mission Planner нужные вам режимы. Используйте эту программу в
качестве мощной наземной станции (Ground Station).

Сотни GPS точек ждут вас (точное число зависит от памяти полетного контроллера,
ArduCopter подерживает 127 точек, но есть и более продвинутые системы на базе PX4).
Просто поставте точку в Mission Planner и ArduCopter полетит к ним.

RTL (Вернуться на старте). Щелкните переключаетелем , что бы вернуть ArduCopter на место старта автоматически.

Планирование всех миссий доступны через опциональную двухстороннюю связь.
Путевые точки, смена режимов полета, даже тюнинг может быть сделан с
вашего ноутбука, в то время как аппарат находиться в воздухе!

Автоматический взлет и посадка. Просто введите аппарат в этот режим
и смотрите как ArduCopter сам выполнит свою миссию полностью автономно,
вернувшись домой сядет на землю перед вами.

В связи с богатым набором функций и полностью автономных возможностей АРМ,
кривая обучения может выглядеть несколько пугающим.
К счастью набор исчерпывающей информации сделает это стремление очень простым и достижимым.

Пожалуйста, не поддавайтесь искушению пропустить шаги и бросаться к быстрому полету.
Это робототехника и авиация комбинированного типа из которых являются довольно
сложными вещи сами по себе. Следуйте инструкциям и у вас будет свой робот
в воздухе.

Подключите радиоприемник: pwm или ppm сигналы

• для управления по радио через ШИМ (PWM) подключите радиоприемник к APM входных сигнальных контактов используя разъемы для подключения канала 1 к APM сигнала конекторами с надпиьсь 1 , канал 2 к конекторам 2 и т.д. Кроме того, необходимо убедиться в том, что приемник будет питаться от APM.
• для управления по радио через PPM необходимо подключить первый канал и перемкнуть перемычкой входы 2 и 3 , как показано на картинке. Выводы на приемнике могут варьироваться , поэтому обратитесь к документации на ваш приемник.

После скачивания и установки Mission Planner на вашу наземную станцию, подключите APM к компьютеру используя микро-USB провод.
Не подключайте провод к USB-хабу , подключайте провод к компьютеру.

После установки Mission Planner подключите через micro-USB APM с системой Windows, которая автоматически определит
и предоставит драйвера для устройства, запустите программное обеспечение и выберите порт который будет указан
в списке, выберите необходимую скорость (по умолчанию это 115200 бод/с) как показано на рисунке

Выберите “соединение” в правом вверхнем углу экрана ,
что бы загрузить параметры MAVLINK в APM ,
Mission Planner будет показывать окно с параметрами загрузки данных.

Когда инициализация параметров пройдёт окно загрузки пропадёт.

Включите передатчик и убедитесь, что он в режиме самолета
(Полетному контроллеру необходим режим полета , независимо от платформы на
эксперементальной основе) и установите все стики по центру.

Левая ручка будет контролировать газ (THR) и рысканья (Yaw),
правая будет контролировать крен (Roll) и тангаж (Pitch) .
Трехпозиционный переключатель будет контролировать режимы полета.

В Mission Planner выберите “Radio Calibrating” ,
нажмите на “калибровка” и правом нижнем углу,
Mission Planner выведет окно,
что батарея не должна быть подключена ,
как и моторы с пропеллерами.

Нажмите “ок” и начните двигать стиками в каждую из сторон до предела,
а так же трехпозиционный тумблер. наблюдайте за результатами,
красные линии установят пределы минимамльного и максимального
значения вашего радиопередатчика.

Когда все значения каналов радио смогли показать свой
минимум и максимум нажмите в программе “Done”.
Данные вам отобразятся в отдельном окне,
нормальное значение около 1100 для минимума и 1900 для максимума.

Советы которые смогут помочь защитить ваш аппарат от повреждений

• 1) избегайте резких и экстремальных полетов
• а) перемещайте стики плавно и не дёргайте их.
• б) если аппарат хорошо сбалансирован и настрое, то он потребует небольшое отклонение стиков, в отличии от “плавающих” и “кривых” аппаратов.
• 2) аппарат должен быть более менее стабильным в горизонтальной плоскости и не иметь дополнительных тримов с аппаратуры.
• а) если коптер “гуляет” в полете, вам прийдется отримировать его с аппаратуры.
• 3) будьте осторожны при подаче большого газа , так как аппарат может получить или потерять высоту (просадка батареи по мощности и нехватка газа на моторы с отключением мозгов и их перезагрузкой).
• 4) так как мультикоптеры симметричны вам очень лего дизарентироваться и потерять его в ориентации.
• а) для ручных полетов ориентация является важной частью для полетов, следите за ней
• б) во время обучения сохранайте орентацию аппарата с момента взлета и контролируйте её.
• в) рекомендуется по началу летать на растояние не более 10м но и не ближе , чем 3 м к себе.
• г) если вы отлетаете дальше чем 30 метров, то очень легко потерять ориентацию в пространстве – это может привети к аварии.
• д) если вы потеряли осевую ориентации (Yaw) во время полета, то попробуйте в режиме стабилизации лететь вперед и спользуя повоторы вокруг оси направлять его как автомобиль.
• е) это гораздо лучше, чем просто спуститься на землю не понимая орентацию, еще хуже – улететь.
• ж) отлетая часто получается , что наклоняя аппарат назад к пилоту вы видете , что он может отдаляться – это происходит из-за потери ориентации.
• з) Результат этого – аппарат улетает и разбивается.
• 5) всегда имейте режим стабилизации на аппаратуре.
• 6) порывы ветра могут сделать полет значительно труднее
• а) сильный ветер может препядствовать движению аппарата или вовсе загрутить его вокруг.
• б) чем выше вы находитесь на местносте , тем больше вероятность сильных ветров.
• в) переключение в режим Стабилизации и посадка позволит вам сохранить аппарат перед тем, как у вас появятся новые навыки пилотирования
• г) Избегайте высоких и скоростных полетов в разных режимов пока не появилась значительная увереность в пилотировании.
• д) при полете вокруг деревьев очень легко потерять визуальный контакт и ориентацию
• е) порывы ветра вокруг объектов, зданий, сооружений могут усугубить пилотирование
• ж) потеря радиосигнала тоже вероятна и может произойти в неподходящий момент.
• з) если ваш аппарат приближается к потенциальной помехе, то следует переключиться на режим стабилизации и вернуть его к себе.
• 7) Ardupilot конкретные спобобы безопасности: RTL, FailSafe , GeoFence
• а) RTL может обеспечить безопасное возращение к месту запуска, если он получит команду от вас.
• б) настройка FailSafe на радиомодуле может быть выполнена командами RTL или Auto Land , что бы сохранить аппарат и предотвратить от травм себя и окружающих.
• в) GeoFence устанвливает автоматический периметр, который заставит аппарат оставаться в безопасном месте.
• г) Не следует пологаться на выше указаные режимы для обеспечения безопасности, у вас всегда должна быть мысль о переводе аппарат в режим стабилизиции и переход в ручное управление, если что-то пойдёт не так.
• д) особенно не пологайтесь на эти режимы выполняя обучение или какие-либо другие маневры.
• е) эти режимы являюся дополнением и не являются заменой в безопасности
• 8) о первом взлете или о настройки контроллера
• а) в режиме стабилизации двигайте стик газа медленно, пока аппарат не зависнет
• б) если аппарат пытается перевернуться – опустите газ и устраните проблемму.
• в) двигатели могут быть настроены в неправильном направлении (см. схемы подключения)
• г) могут быть неправильно установлены пропеллеры
• д) если аппарат пытается крутиться вокруг своей оси или улететь в некотором направлении
• е) передатчик или настройки аппаратуры могут быть не правильными
• ж) двигатели или регуляторы могут быть настроены не правильно
• з) не правильные пропеллеры могут быть надеты не правильно на моторы

и) если аппарат не может висеть стабильно над землей на уровне 2м то стоит решить эту проблему.

• 9) при полете FPV (вид от первого лица) с видеокамерой , вы должны иметь режимы: стабилизация , simple mode и RTL
• а) убедитесь, что RTL работает правильно перед использованием FPV
• б) используйте режим стабилизации при FPV полетах
• в) Если видеосвязь FPV прервалась вы можите переключить на simple mode или RTL для возращения домой.
• 10) убедитесь, что Ваш аккумулятор закреплен надежно
• а) используйте крепление-липучки
• б) можно использовать вклеенну поддержку для батареи для лучшего держания липучки.