Стабилизация квадрокоптера на заданном удалении от объекта. дипломная (вкр). физика. 2023-07-06
Стабилизация квадрокоптера на заданном удалении от объекта
Введение
Квадрокоптер является беспилотным летательным
аппаратом (БЛА). Он представляет собой платформу с четырьмя роторами, одна пара
которых вращается по часовой стрелке, другая – против часовой стрелки. По
сравнению с БЛА вертолетного типа с несущим и рулевым винтами, квадрокоптеры
обладают рядом преимуществ, таких как: надежность и простота конструкции,
большая стабильность, компактность и маневренность, малая взлетная масса при
существенной массе полезной нагрузки.
Область применения квадрокоптеров достаточно
широка. Он может быть использован как недорогое и эффективное средство для
получения фото и видео изображений с воздуха, в том числе в плохих погодных
условиях. Благодаря тому, что квадрокоптер дистанционно управляемый летательный
аппарат, он хорошо подходит для наблюдения и контроля объектов и зон, доступ к
которым затруднен (например, в случае естественных или техногенных катастроф)
или в условиях непригодных для человека, таких как повышенный уровень радиации
или сильное загрязнение воздуха.
Основной задачей управления таким БЛА является
его стабилизации в условиях воздействия внешних возмущающих факторов, таких как
сильный порывистый ветер.
Цель работы:
разработка алгоритма стабилизации квадрокоптера
на заданном расстоянии от объекта на основе комплексной обработки информации,
получаемой от двух разнесённых видеокамер и датчиков положения БЛА
(акселерометры, гироскопы);
исследование эффективности разработанного
алгоритма с применением математической модели мультикоптера, разработанной в
системе MatLab.
1.Объект исследования
.1 Устройство и принцип работы
квадрокоптера
Квадрокоптер представляет собой платформу с
четырьмя роторами. Центральная часть квадрокоптера служит для размещения
контроллера, батареи и полезной нагрузки (например, видеокамеры). Радиально от
центра на балках устанавливаются микроэлектродвигатели с несущими винтами,
образуя крестообразную конструкцию аппарата.
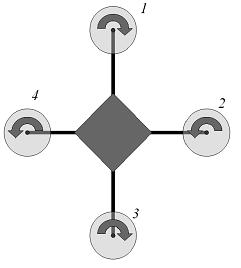
Рис. 1.1. Схематическое изображение
квадрокоптера
Во время полета квадрокоптер поддерживает
горизонтальное положение относительно земли, может парить на месте, вращаться
относительно вертикальной оси, перемещаться в любом направлении. Для
компенсации вращающего момента, вызванного вращением роторов, у квадрокоптера
1-й и 3-й роторы вращаются по часовой стрелке, а 2-ой и 4-ый – против часовой
стрелки. Для того чтобы квадрокоптер начал движение необходимо вывести его из
состояния баланса путем увеличения силы тяги (скорости вращения) части
пропеллеров, в результате квадрокоптер наклоняется и начинает движение в нужном
направлении. Для поворота квадрокоптера вокруг своей оси необходимо ускорить
вращение одной пары пропеллеров вращающихся в одном направлении и замедлить
вращение другой пары пропеллеров.
Например, чтобы повернуть аппарат вокруг своей
оси против часовой, 1-й и 3-й роторы должны вращаться быстрее, а 2-й и 4-й
роторы должны замедлиться. Основные режимы полета и стабилизация квадрокоптера
обеспечивается с помощью контроллера размещенного на нем. Контроллер на
основании данных полученных от датчиков при помощи специальной программы
рассчитывает скорости вращения роторов и подает на двигатели соответствующие
управляющие сигналы. Минимальным набором датчиков необходимых для стабилизации
квадрокоптера являются акселерометры – для измерения ускорения и гироскопы –
для определения углов наклона. Кроме того, квадрокоптер может быть оборудован
барометром, магнитомером (компасом) и даже GPS-навигатором.
1.2 Постановка задачи
Задача состоит в том, чтобы при наблюдении за
объектом стабилизировать квадрокоптер на некотором расстоянии от него. Причем
стабилизации должна заключаться не только в стабилизации летательного аппарата
как материальной точки, но и в стабилизации квадрокоптера по направлению, т.к.
для наблюдения необходимо, чтобы видеокамеры были направлены на объект.
Таким образом, необходимо на автопилоте или
ручном управлении приблизить квадрокоптер на некоторое расстояние до цели, при
этом по стереозибражению с оптических камер будет вычисляться в реальном
масштабе времени расстояние до цели. Как только квадрокоптер приблизиться на
достаточное расстояние на его контроллер будет передан сигнал, который передаст
управление квадрокоптером программе стабилизации, которая выберет точку в
пространстве и затем стабилизирует в ней летательный аппарат.
2.Модель квадрокоптера
.1 Системы координат
При практическом использовании уравнений
движения БЛА их записывают в проекциях на оси выбранных систем координат (СК).
В данной работе удобно использовать две правых прямоугольных системы координат,
назовем их неподвижной и подвижной системами координат:
. Неподвижная система координат. Начало
находиться в точке O, в которой необходимо стабилизировать квадрокоптер. Оси OX
и OY расположены в горизонтальной плоскости, а ось OZ направлена вверх.
2. Подвижная система координат.
Начало находиться в центре масс квадрокоптера, в точке 
. Оси этой системы координат: 
, 
и 
сонаправлены с осями координат
неподвижной СК. Таким образом, подвижная СК получается из неподвижной СК
параллельным переносом на радиус вектор 
центра масс квадрокоптера в
неподвижной СК.
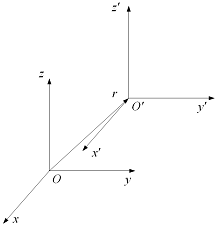
Рис. 1.2. Неподвижная и подвижная
системы координат
2.2 Момент инерции
Пусть квадрокоптер лежит в плоскости
OXY, его центр масс находиться в точке O, а балки AC и BD, на которых
расположены роторы, лежат вдоль осей OX и OY. Момент инерции квадрокоптера
одинаков вокруг любой оси MN, лежащей в плоскости квадрокоптера OXY. Обозначим
массу квадрокоптера как 
. Пусть масса каждого ротора
сосредоточена в точках A, B, C и D и равна 
, а вся масса корпуса равномерно
распределена на отрезках АС и BD и равна 
.
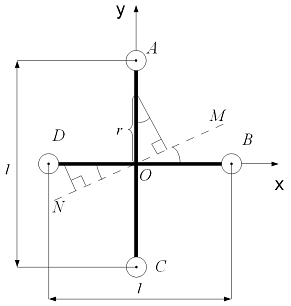
Рис. 1.3. Расчет момента инерции
Тогда момент инерции квадрокоптера относительно
любой оси MN составляющей с осью BD угол α
равен:
(2.2.1) 
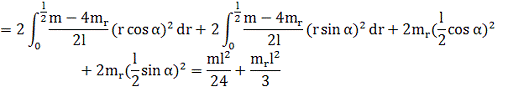
Момент инерции относительно оси OZ,
перпендикулярной плоскости OXY и проходящей через точку O,
вычисляется по формуле:
(2.2.2) 
2.3 Уравнения
движения
Квадрокоптер, как и любое твердое тело, является
системой с шестью степенями свободы, соответственно для описания его движения
требуется шесть независимых числовых уравнений или два векторных уравнения.
Уравнения движения центра масс
Вектор силы тяжести приложен к
центру масс квадрокоптера и имеет вид: 
, где 
– ускорение свободного падения.
Сила сопротивления воздуха 
, где 
– безразмерный аэродинамический
коэффициент, 
– плотность воздуха, 
– площадь поверхности. Таким
образом, сила сопротивления воздуха пропорциональна квадрату скорости с
некоторым коэффициентом 
и направлена противоположно
скорости.
Вектор суммарной силы тяги всех
роторов также приложен к центру масс и имеет вид: 
, где 
, 
, 
и 
– силы тяг первого, второго,
третьего и четвертого роторов соответственно
Вектор некоторой посторонней силы
обозначим как 
. В случае когда сила вызвана ветром 
, так как сила, с которой действует
ветер на квадрокоптер фактически является силой сопротивления воздуха.
Таким образом, векторное уравнение
описывающее движение цента масс квадрокоптера в неподвижной системе координат
имеет вид:
Скорость можно получить выразив
ускорение и проинтегрировав его по времени:
Проинтегрировав скорость, получается
радиус вектор до центра масс квадрокоптера, т.е. координаты положения центра
масс квадрокоптера:
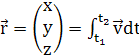
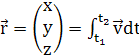
Уравнение моментов:
Уравнение моментов в данном случае
удобно рассматривать относительно центра масс, в подвижной системе координат.
Уравнение моментов описывает вращение тела относительно мгновенной оси. В этой
модели вращение может быть вызвано только силами, которые создают роторы.
Введем векторы
, 
,
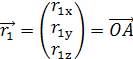
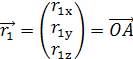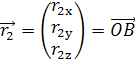
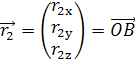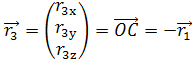
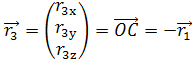и 
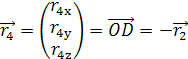
– радиус векторы роторов в подвижной
системе координат. Длины этих векторов равны между собой и равны 
.
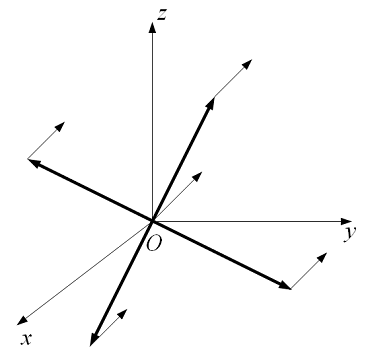
Рис. 1.4. Схематическое изображение
квадрокоптера в подвижной СК
В данном случае удобней разбить это уравнение на
два: первое уравнение будет описывать вращение вокруг оси симметрии
квадрокоптера, второе уравнение будет описывать вращение вокруг оси лежащей в
плоскости квадрокоптера. Тогда первое уравнение имеет вид:
Выразив угловое ускорение из этого
уравнения и проинтегрировав его по времени, можно получить угловую скорость:
,
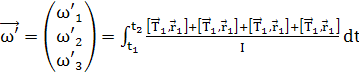
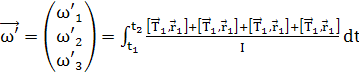где 
, 
и 
в – компоненты вектора 
по осям координат.
Проинтегрировав по времени угловую
скорость, можно получить углы поворота квадрокоптера вокруг осей подвижной СК:
,
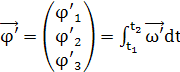
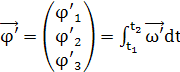где компоненты 
, 
и 
вектора 
представляют собой углы поворота
вокруг осей нормальной системы координат OX, OY и OZ соответственно.
Рассмотрим вращение квадрокоптера
вокруг оси перпендикулярной плоскости. Обозначим реактивный момент винтов как 
. Вектор этого зависит только от
величины 
и направлен вдоль нормали к
плоскости квадрокоптера. Кроме реактивного момента существует еще сонаправленый
ему момент сил, вызванный гироскопическим эффектом из-за изменения
гироскопических моментов роторов, который тоже может вращать корпус
квадрокоптера вокруг этой оси, но так как роторы вращаются в разных
направлениях его можно не рассматривать. Тогда модуль углового ускорения
выражается формулой:
,
Где 
– некоторая функция зависящая от
величины .
Проинтегрировав это выражение можно
получить модуль угловой скорости, при этом полученная угловая скорость всегда
будет направлена перпендикулярно плоскости квадрокоптера. Обозначим единичный
вектор направленный перпендикулярно плоскости квадрокоптера как 
. Таким образом, получаем:
А проинтегрировав это уравнение
получается углы поворота квадрокоптера вокруг осей подвижной СК.
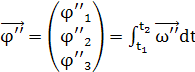
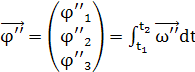
Таким образом, суммарные значение
угловой скорости и углов поворота будут равны:
3.Алгоритм
.1 Стабилизация квадрокоптера как
материальной точки
Пусть центр масс квадрокоптера
находиться в точке М с радиус вектором 
. Пусть квадрокоптер перемещается со
скоростью 
, на него действуют внешняя сила 
. Требуется стабилизировать
квадрокоптер в точке O. Примем точку O за начало неподвижной системы координат.
Будем рассматривать квадрокоптер как материальную точку с массой . Для того чтобы стабилизировать
квадрокоптер требуется подействовать на него с некоторой силой 
.
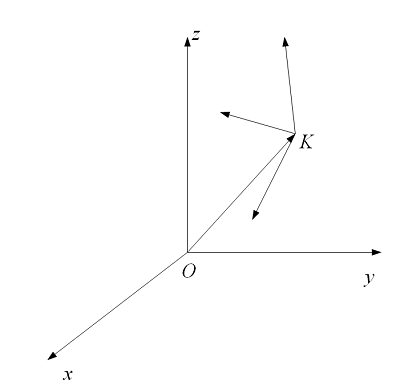
Рис.
Для стабилизации достаточно
эффективным является пропорционально дифференциальный алгоритм. Суть его в том,
что для того чтобы стабилизировать тело в точке О сила должна состоять из двух
составляющих:
· составляющей пропорциональной отклонению от
точки стабилизации с некоторым коэффициентом 
· составляющей пропорциональной с некоторым
коэффициентом 
производной от отклонения,
где коэффициенты и определяются экспериментально.
Кроме того необходимо компенсировать
внешнюю силу. Таким образом, требуемая сила должна быть равна:
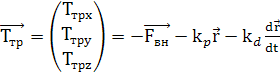
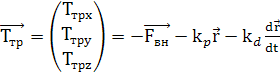
Таким образом, необходимо чтобы
суммарная сила тяги роторов квадрокоптера равнялась вектору . Так как сила тяги роторов всегда
направлена по нормали к плоскости квадрокоптера, необходимо повернуть плоскость
квадрокоптера так, чтобы нормальный к ней вектор 
был направлен вдоль . То есть решить задачу стабилизации
квадрокоптера по углу.
3.2 Стабилизация квадрокоптера по
углу
Положение квадрокоптера относительно связанной
системы координат удобно определять с помощью трех углов поворота относительно
осей подвижной СК. Требуемые значения углов, на которые необходимо повернуть
квадрокоптер относительно каждой из осей нормальной системы координат,
вычисляются по следующим формулам:
Где 
,
и 
– повороты вокруг осей OX, OY и OZ
соответственно.
При этом направление вектора нормали
определяется двумя углами, а именно поворотом вокруг осей OX и OY. Уравнениями
(2.3.12) определяются текущие значения этих углов: и 
соответственно. Таким образом,
задача сводится к тому, чтобы стабилизировать плоскость квадрокоптера углам и . Эту задачу тоже удобно решать
пропорционально-дифференциальным алгоритмом. Углы поворота определяются составляющими
вектора 
по осям OX и OY соответственно.
Таким образом, в качестве управляющего воздействия для стабилизации по углу можно рассматривать разность
векторов и спроецированную на плоскость OYZ, а
для – разность векторов и спроецированную на плоскость OXZ.
Тогда для стабилизации по углу 
пропорциональной составляющей будет
разность между и , взятая с коэффициентом 
, а дифференциальной – составляющая
по оси OX вектора 
, определенного по формуле (2.3.11),
взятая с коэффициентом 
. Аналогично для стабилизации по
углу . Величину проекции вектора на
плоскость OYZ можно найти, умножив значение его длинны на косинус угла между
вектором нормали и плоскостью. Этот значение этого косинуса равно 
. Аналогично можно найти проекцию на
плоскость OXZ. Таким образом, окончательно имеем:
Суммарная сила тяги должна плавно
меняться от некоторого начального значения 
до требуемого 
, тогда
,
где 
и 
начальные значения углов и соответственно.
Для того чтобы наблюдать за объектом
нам необходимо чтобы камеры были направлены на него. Камеры будут направлены на
объект, если у векторов 
и 
компоненты по оси OY и OX
соответственно будут стремиться к нулю. Этого можно достичь, управляя вращением
в плоскости квадрокоптера. В этом случае в роли управляющего воздействия будет
разность между суммами тяг роторов вращающихся по часовой стрелке и роторов
вращающихся против часовой стрелки. В качестве пропорциональной составляющей мы
возьмем значение сумму значений 
и 
, домноженную на коэффициент 
, а в качестве дифференциальной
производную от этой суммы, домноженную на коэффициент 
. Таким образом, получаем:
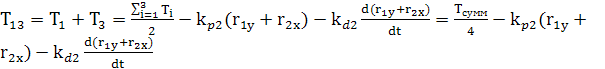
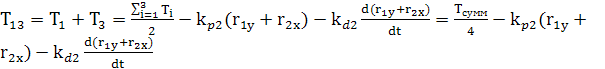
Уравнения (3.2.4), (3.2.5), (3.2.7) и (3.2.8)
составляют систему из четырех уравнений с четырьмя неизвестными, решив ее можно
получить выражения для тяг на каждом роторе. Таким образом:
Так как неизвестен реактивный момент
квадрокоптера данный алгоритм не будет реализовывать стабилизацию квадрокоптера
по направлению. Поэтому в данном алгоритме примем 
.
4.Программная реализация модели
квадрокоптера и пример работы
.1 Программная реализация модели
квадрокоптера
Модель реализована на языке MatLab и состоит из
трех подпрограмм:
) Основная программа рассчитывает радиус
вектор из точки стабилизации до центра масс квадрокоптера и выводит графики
зависимости координат центра масс квадрокоптера в неподвижной СК от времени.
) Блок вычисления текущего значения тяги
– подпрограмма, которая на основе рассчитанной требуемой силы тяги вычисляет
силы тяги на каждом роторе и вычисляет значения суммарной силы тяги в
определенные моменты времени
) Блок расчета силы внешнего воздействия
– подпрограмма, вычисляющая значение силы внешнего воздействия в конкретный
момент времени. Третья подпрограмма просто представляет собой вектор функцию от
времени. На первых двух подпрограммах остановимся подробней.
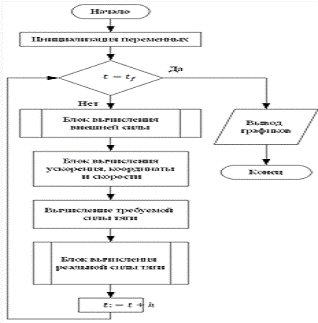
Рис. 4.1.1. Блок схема основной программы
В блоке инициализация переменных
задается начальное значение времени 
и начальные значения скорости , радиус вектора 
центра масс квадрокоптера и
начальные значение суммарной тяги роторов 
в неподвижной СК, а также значения
начальные угловой скорости и углов поворота квадрокоптера в подвижной СК.
Внутри цикла в первом блоке вычисляется значения внешней возмущающей силы 
в моменты времени 
, 
и 
и заносятся в переменные 
, 
и 
. В следующем блоке по формуле
(2.3.1) вычисляются значения ускорения 
в моменты времени , 
и 
:
Затем с помощью интегрирования от
нуля до текущего значения времени вычисляются текущие значения
скорости и радиус-вектора по формулам (2.3.2) и (2.3.3). Интегрирование
осуществляется методом Рунге-Кутты. Для этого применяются формулы:
,
Где
В следующем блоке, исходя из
полученных значений радиус вектора, скорости и внешней силы по формуле (3.1.1)
вычисляется требуемое значение силы тяги . Затем на блок вычисления текущего
значения силы тяги подаются переменные , , . На выходе блока получаем значения и в следующий момент времени 
, и значения суммарной силы тяги 
, 
и 
в моменты времени 
, 
и 
, необходимые для интегрирования
методом Рунге-Кутты. Затем увеличиваем t на h и подаем полученные значения на
начало цикла. Это повторяется до тех пор, пока не будет достигнуто время 
. Блок вычисления текущего значения
тяги
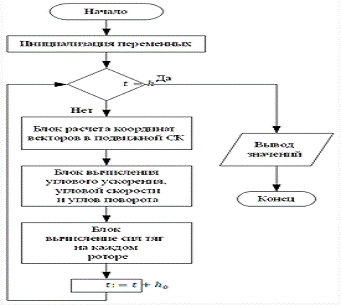
Рис. 4.1.1. Блок схема блока вычисления текущего
значения тяги
На вход подаются: , и . Внутренней переменной времени
присваивается значение ноль: 
.
Внутри цикла в первом блоке, исходя
из значения , вычисляются матрицы поворота:
,
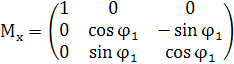
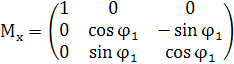
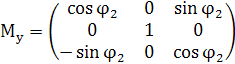
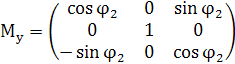
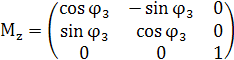
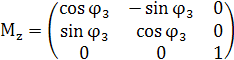
где 
, 
и 
– матрицы поворота вокруг осей OX,
OY и OZ соответственно, а 
-матрица композиции поворотов
вокруг трех осей.
Затем пересчитываются координаты
векторов , , , и 
, 
, 
, 
по формулам:
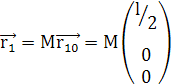
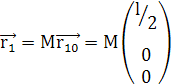
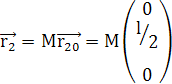
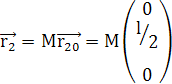
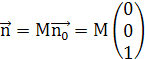
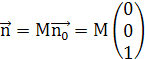
(4.1.16) 
(4.1.17) 
(4.1.18) 
Затем вычисляется значение суммарной
силы тяги роторов:
Используя полученные значения во
втором вычисляется угловое ускорение по формуле (2.3.5) затем угловую скорость 
по формуле (2.3.6) и углы поворота
вокруг осей подвижной СК 
по формуле (2.3.7).
В следующем блоке рассчитываются
значения тяг на каждом роторе по формулам (3.2.9), (3.2.10), (3.2.11) и
(3.2.12). На первом шаге записывается выходное значение 
, когда 
записываются выходные значения 
, когда 
записывается выходное значение 
. Затем время увеличивается на шаг 
и подается на начало цикла. Если цикл завершается и на выходе
подпрограмма выдает значения , и и конечные значения и .
4.2Пример использования
По формуле (2.2.1) момент инерции
равен 
. Для расчетов коэффициент
пропорциональности 
между силой сопротивления воздуха и
квадратом скорости квадрокоптера был принят равным 
.
Шаг интегрирования в основной
программе был принят равным 
, шаг интегрирования в блоке
вычисления текущего значения силы тяги 
.
Экспериментально были получены
константы 
, 
, 
и 
.
Таблица1. Константы
Пример 1
В данном случае в начальный момент
времени квадрокоптер находится в точке 
с координатами (0 0 0) и скоростью 
в неподвижной СК. На квадрокоптер
действует ветер, скорость которого равна 
, то есть скорость ветра по модулю
равна 12,64 м/с. Рассмотрим два случая: с использованием алгоритма стабилизации
и без использования.
1) Графики зависимости от времени координат
центра масс квадрокоптера и проекций его скорости на оси при отсутствии
стабилизации имеют вид:
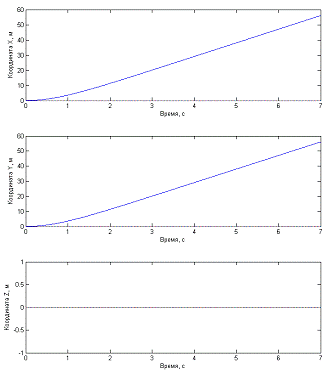
Рис. 4.2.1 Графики зависимости координат центра
масс квадрокоптера от времени при отсутствии стабилизации
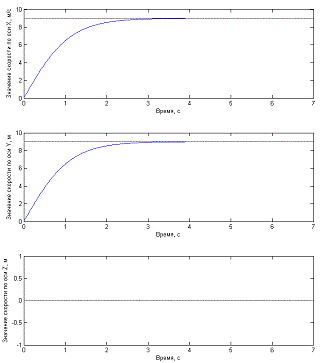
Рис. 4.2.2 Графики зависимости компонент вектора
скорости центра масс квадрокоптера от времени при отсутствии стабилизации
2) Со стабилизацией при тех же начальных данных
графики зависимости координат от времени имеют вид:
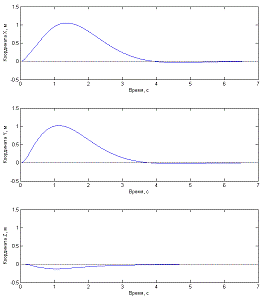
Рис. 4.2.3 Графики зависимости координат центра
масс квадрокоптера от времени при использовании алгоритма стабилизации
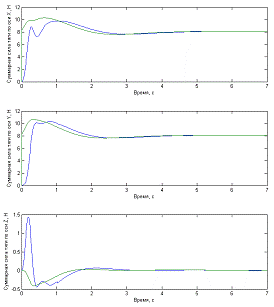
Рис. 4.2.4 Графики зависимости компонент
суммарной силы тяги по осям от времени. Синими линиями показана зависимость
реальной силы тяги, а зелеными – требуемой.
Пример 2
Имеет смысл рассмотреть более сложный пример.
Пусть начальная скорость
квадрокоптера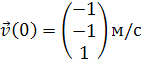 
.
Начальный радиус вектор центра масс
квадрокоптера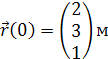 
Пусть сила, с которой действует на
квадрокоптер ветер равна
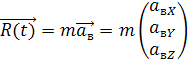
Для моделирования порывистого ветра
удобно задать зависимостью ускорения, которое он сообщает квадрокоптеру, от
времени.
Таблица 2. Ускорение переданное квадрокоптеру
внешней силой
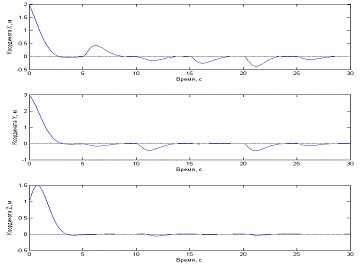
Рис. 4.2.5 Графики зависимости координат
центра масс квадрокоптера от времени при использовании алгоритма стабилизации
для примера 2.
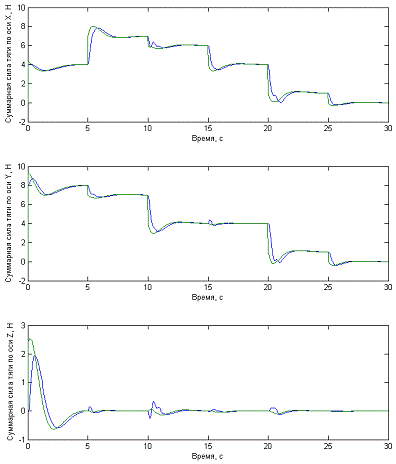
Рис. 4.2.6 Графики зависимости компонент
суммарной силы тяги по осям от времени для примера 2. Синими линиями показана
зависимость реальной силы тяги, а зелеными требуемой.
Заключение
Целью данной работы является разработка и
исследование алгоритма стабилизации квадрокоптера. Для достижения данной цели
были решены следующие задачи:
) Разработана математическая модель
квадрокоптера
) Разработан алгоритм стабилизации
квадрокоптера для этой модели
) Выполнена программная реализация
разработанной математической модели в системе MatLab и проведено исследование
алгоритма с использованием полученной модели.
В ходе исследования были получены оптимальные
коэффициенты необходимые для работ алгоритма и проверена его работа для различных
условий. Данный алгоритм требует более детальной проверки с учетом более точной
и достоверной модели. В качестве возможных направлений дальнейшего развития
математической модели квадрокоптера можно отметить следующие:
) Усовершенствование уравнения движения
центра масс квадрокоптера с учетом таких факторов как:. Более точный
расчет силы сопротивления воздуха. Более сложная модель ветра
) Усовершенствование уравнения моментов
для вращения квадрокоптера с учетом таких факторов как:. Исследование
реактивного момента роторов и вывод уравнения вращения квадрокоптера вокруг оси
перпендикулярной плоскости квадрокоптера. Расчет влияния гироскопического
эффекта вызванного вращением роторов. Сложная геометрическая форма
квадрокоптера
) Исследование эффективности
предложенного алгоритма стабилизации квадрокоптера по направлению.
квадрокоптер летательный аппарат
Литература
.Беклимишев
Д.В. Курс аналитической геометрии и линейной алгебры – Издание 11-е,
исправленное – М: Физматлит, 2006.
.Сивухин
Д.В. Общий курс физики. Учебное пособие: Для вузов. В 5 т. Т Ι.
Механика
– Издание 5-е, стереотипное – М: Физматлит, 2002.
.Лазарев
Ю. Моделирование процессов и систем в MATLAB. Учебный курс. – Спб.: Питер;
Киев: Издательская группа BHV, 2005.
.Денисенко
В.В. ПИД-регуляторы: принципы построения и модификации – Современные технологии
автоматизации. 2006. № 4. С. 66 – 74; 2007. № 1. С. 78 – 88.
