Классификация связей: голономные, стационарные и удерживающие. виртуальное перемещение точки. виртуальная работа. идеальная связь.
Связь называется голономной, если в уравнение связи входят только координаты точек механической системы или иные параметры, определяющие ее положение в пространстве. 
Связь называют удерживающей, если она выражается математически равенством, и неудерживающей, если она выражается неравенством.
Связь называется стационарной, если в уравнение связи время явно не входит. Если в уравнение связи время входит явным образом, то связь − нестационарная.
Примером нестационарной связи, наложенной на материальную точку, является нить, длина которой изменяется согласно некоторому закону  . Это голономная, неудерживающая, нестационарная связь.
. Это голономная, неудерживающая, нестационарная связь.
Виртуальным (возможным) перемещением точки (обозначается 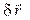 ) называется такое бесконечно малое (элементарное) перемещение, которое допускается в рассматриваемый момент движения наложенными на точку связями.
) называется такое бесконечно малое (элементарное) перемещение, которое допускается в рассматриваемый момент движения наложенными на точку связями.
Проекции вектора виртуального перемещения точки 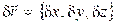 называются вариациями координат.
называются вариациями координат.
В случае голономной нестационарной связи уравнение 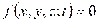 в фиксированный момент определяет некоторую поверхность в трехмерном пространстве, на которой находится движущаяся точка. Виртуальные перемещения лежат в касательной плоскости к этой поверхности и вариации координат удовлетворяют уравнению
в фиксированный момент определяет некоторую поверхность в трехмерном пространстве, на которой находится движущаяся точка. Виртуальные перемещения лежат в касательной плоскости к этой поверхности и вариации координат удовлетворяют уравнению 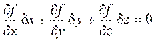 ,
,
выражающему перпендикулярность вектора нормали к поверхности 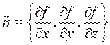 и вектора
и вектора 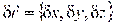 .
.
Виртуальным перемещением механической системы называется совокупность виртуальных перемещений точек этой системы.
Например, виртуальным перемещением кривошипно-ползунного механизма, являются два элементарных поворота – кривошипа на угол 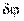 вокруг оси вращения и шатуна на угол
вокруг оси вращения и шатуна на угол 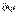 вокруг мгновенного центра скоростей. Из геометрических соображений следует, что:
вокруг мгновенного центра скоростей. Из геометрических соображений следует, что:  . Связь между виртуальными перемещениями отдельных тел и точек, образующих механическую систему, в общем случае может быть найдена аналитически путем варьирования уравнений связи.
. Связь между виртуальными перемещениями отдельных тел и точек, образующих механическую систему, в общем случае может быть найдена аналитически путем варьирования уравнений связи.
Виртуальной работой силы(обозначается 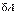 )называется работа силы на виртуальном перемещении точки ее приложения, т.е.:
)называется работа силы на виртуальном перемещении точки ее приложения, т.е.:  .
.
Связь называется идеальной, если сумма работ реакций этой связи на любом виртуальном перемещении системы равна нулю.
 Примером является шероховатая поверхность для катка, катящегося без скольжения, при отсутствии трения качения
Примером является шероховатая поверхность для катка, катящегося без скольжения, при отсутствии трения качения 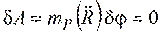 .
.
Принцип виртуальных перемещений.
Для равновесия механической системы с идеальными и стационарными связями необходимо и достаточно, чтобы сумма виртуальных работ всех активных сил, приложенных к точкам системы, была равна нулю
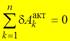
Дано, что механическая система находится в равновесии и требуется доказать, что  . Так как система находится в равновесии, то равнодействующая активных сил
. Так как система находится в равновесии, то равнодействующая активных сил  и равнодействующая сил реакций связей
и равнодействующая сил реакций связей 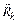 , приложенных в
, приложенных в 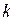 -й точке системы, удовлетворяют условию равновесия статики:
-й точке системы, удовлетворяют условию равновесия статики:
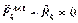 ,
, 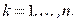
Пусть  , докажем, что механическая система находится в равновесии. Предположим, что при заданных условиях система не находится в равновесии, т. е. при действии на систему активных сил хотя бы одна точка получила действительное перемещение
, докажем, что механическая система находится в равновесии. Предположим, что при заданных условиях система не находится в равновесии, т. е. при действии на систему активных сил хотя бы одна точка получила действительное перемещение 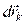 и
и 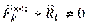 .
.
Так как для стационарных связей действительное перемещение совпадает с одним из возможных (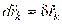 ), то
), то  или
или 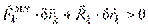 по крайней мере для одной точки системы, вышедшей из равновесия. Суммируя по всем точкам системы, получаем
по крайней мере для одной точки системы, вышедшей из равновесия. Суммируя по всем точкам системы, получаем 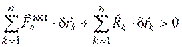 .
.
Так как связи идеальные, то 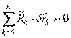 Þ
Þ 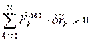 Þ
Þ 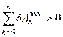 , что противоречит условию.
, что противоречит условию.
Следовательно, система находится в равновесии.
Принцип виртуальных перемещений может быть записан в иной форме, если поделить уравнение, выражающее этот принцип на временной интервал 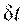 , в течение которого совершается это перемещение.
, в течение которого совершается это перемещение.
Общее уравнение динамики.
Рассмотрим систему, состоящую из N материальных точек, с идеальными и голономными связями, положение которой однозначно определяется s обобщенными координатами 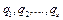 . Запишем для каждой точки системы основное уравнение динамики
. Запишем для каждой точки системы основное уравнение динамики
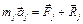
или
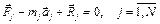 .
.
Зафиксируем время и дадим системе виртуальное перемещение, при котором радиус-векторы точек получат приращения 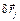 . Умножим скалярно каждое уравнение на
. Умножим скалярно каждое уравнение на 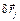 и сложим полученные произведения
и сложим полученные произведения
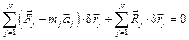
Так как связи идеальные, последняя сумма равна нулю и из уравнения получим
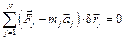
Учитывая, что 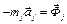 – это сила инерции j-й материальной точки,
– это сила инерции j-й материальной точки, 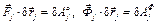 – работы активной силы и силы инерции, перепишем равенство в виде:
– работы активной силы и силы инерции, перепишем равенство в виде:
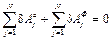 .
.
Это уравнение называют общим уравнением динамики. Оно утверждает, что при движении системы с идеальными связями в любой момент времени сумма работ активных сил и сил инерции на любом виртуальном перемещении системы равна нулю.
Связи и их классификация. идеальные связи
В аналитической механике широко используются понятия: «механическая система»; «связи», наложенные на механическую систему. Уточним эти понятия и проведём их классификацию.
Связи – материальные тела, осуществляющие ограничения, налагаемые на положения и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах.
Эти ограничения записываются в виде уравнений или ограничений.
Уравнения связей – уравнения, которым в силу наложенных связей должны удовлетворять координаты точек механической системы и их скорости (первые производные от координат по времени).
Геометрические связи – связи, уравнения которых содержат только координаты точек механической системы.
Эти связи выполнены в виде тел, поверхностей, линий и т. п. Например, связь в виде некоторой поверхности описывается уравнением f(X, Y, Z) = 0.
Дифференциальные связи – связи, уравнения которых, кроме координат точек механической системы, содержат ещё первые производные от этих координат по времени.
Уравнение такой связи имеет вид
f(X, Y, Z, dX/dt, dY/dt, dZ/dt) = 0.
Голономные связи – геометрические связи и дифференциальные связи, уравнения которых можно проинтегрировать.
Неголономные связи – дифференциальные связи, уравнения которых не могут быть проинтегрированы.
Стационарные связи – связи, в уравнения которых время явно не входит.
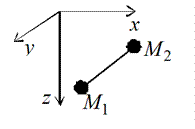
Например, геометрическая стационарная связь в виде невесомого стержня длины l, ограничивающая перемещение материальной точки (рис. 6.11), описывается уравнением

X2 Y2 Z2 – l2 = 0.
Если в рассматриваемом примере (рис. 6.11) вместо стержня будет нить, длина которой с течением времени изменяется, то такая связь будет геометрически нестационарной. Эта связь описывается уравнением
X2 Y2 Z2 – l2(t) = 0.
Двусторнние (удерживающие) связи – связи, допускающие возможные перемещения только в двух взаимно противоположных направлениях.
Примером такого типа связи служит, например, кулисный камень. Эти связи описываются уравнением f(X, Y, Z, t) = 0.
Односторонние (неудерживающие) связи – связи, при которых точки механической системы имеют возможные перемещения, противоположные которым не являются возможными.
К связям такого типа относится, например, шарнирно-подвижная опора. Аналитически эти связи описываются неравенствами типа f(X, Y, Z, t) ≥ 0.
Механическая система – любая совокупность материальных точек, движения которых взаимозависимы.
Голономная система – механическая система, на которую наложены голономные связи.
Неголономная система – механическая система, на которую наложена хотя бы одна неголономная связь.
Возможное перемещение системы – любая совокупность возможных перемещений точек данной механической системы, допускаемая всеми наложенными на неё связями.
Рассмотрим понятие «возможная работа силы», которое также широко применяют в аналитической механике.
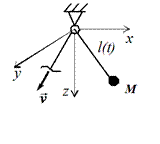
Возможная (элементарная) работа силы – бесконечно малая величина, равная скалярному произведению вектора силы F на вектор возможного перемещения δS точки её приложения.

На рис. 6.12 показаны векторы F и δS.
Согласно рис. 6.12 и определению возможную работу δA(F) силы F определяют по формуле
δA(F) = F·δS = F·δS·cos(F, δS) = F·δS·cos(α).
В зависимости от величины угла α возможная работа δA(F) может быть положительной, отрицательной или равной нулю.
Рассмотрим случай, при котором под действием силы F тело совершает вращательное движение относительно оси ОХ (рис. 6.13).
При вращении тела возможную работу δA(F) силы F на возможном угловом перемещении δφ в общем случае определяют по формуле
δA(F) = ± МОХ(F)·δφ = ± (F·h)·δφ,
где МОХ(F) – момент силы F относительно оси ОХ вращения; h – плечо силы F относительно оси вращения.
Следует отметить, что при совпадении направления МОХ(F) и δφ возможная работа δA(F) > 0. Если направления МОХ(F) и δφ противоположны, то δA(F) < 0.
Возможная элементарная работа δAS сил, приложенных к точкам механической системы, вычисляется по формуле
δAS = ΣδA(Fi).
Рассмотрим еще одно понятие «идеальные связи», применяемое в аналитической механике.
Идеальные связи – связи, для которых сумма элементарных работ их реакций равна нулю на любом возможном перемещении механической системы.
Идеальными связями являются: гладкая поверхность; шарнирно-подвижная и шарнирно-неподвижная опоры; шероховатая поверхность при качении по ней рассматриваемого тела и др.
§
При решении задач на равновесие механических систем, например, для составной конструкции применяются соответствующие уравнения равновесия. Как правило, такие задачи являются статически неопределимыми. Для их решения требуется рассматривать равновесие каждого из тел системы под действием активных сил, реакций внешних связей и реакций внутренних связей. В результате того, что для каждого из тел системы составляются уравнения равновесия, приходится решать большие системы уравнений. Такой подход к решению задачи становится громоздким и потому малопригодным. В этих случаях целесообразно использовать принцип возможных перемещений, который существенно облегчает решение поставленной задачи.
Формулировкапринципа возможных перемещений.
Для равновесия механической системы, на которую наложены стационарные идеальные связи, необходимо и достаточно, чтобы сумма работ активных (задаваемых) сил на любых возможных перемещениях механической системы равнялась нулю.
Этот принцип выражается формулой
δA = ΣδA(Fi) = ΣFi·δSi = ΣFi·δSi·cos(Fi, δSi) = 0,
где Fi – активная сила, приложенная к i-й точке механической системы; δSi – возможное перемещение точки приложения силы Fi.
Принцип возможных перемещений в декартовой системе отсчёта имеет вид
Σ(FiOX·δSiOX FiOY·δSiOY FiOZ·δSiOZ) = 0,
где FiOX, FiOY, FiOZ – проекции задаваемых (активных) сил на координатные оси; δSiOX, δSiOY, δSiOZ – проекции возможных перемещений δSi точки приложения сил Fi на координатные оси.
Если предыдущую формулу (ΣFi·δSi = ΣFi·δSi·cos(Fi, δSi) = 0) продифференцировать по времени, то получим
ΣFi·Vi = ΣFi·Vi·cos(Fi, Vi) = 0,
где Vi = d(δSi)/dt – возможная скорость точки приложения силы Fi.
Так как по определению F·V = F·V·cos(F, V) = N, где N – мощность, то последнее равенство трактуют как принцип возможных скоростей или принцип возможных мощностей.
Для равновесия механической системы, на которую наложены стационарные идеальные связи, необходимо и достаточно, чтобы сумма мощностей активных сил на любых возможных скоростях точек этой системы равнялась нулю.
Для закрепления изложенного теоретического материала рекомендуется выполнить курсовые задания Д 6, Д7.
6.3.1. Варианты курсового задания Д 6
«Применение принципа возможных перемещений
к решению задач о равновесии сил, приложенных
к механической системе с одной степенью свободы»
Схемы механизмов, находящихся под действием взаимно уравновешивающихся сил, и необходимые для расчёта данные приведены в табл. 5.4. В расчётах использовать следующие условные обозначения: с – коэффициент жёсткости пружины (Н/см); h – деформация пружины (см); Q, P – силы (Н); М – момент пары сил (Н·м).
Примечания:
Вариант 6. Вес рукоятки О1А не учитывать.
Вариант 7. Пружина сжата.
Вариант 8. Пружина сжата.
Вариант 10. Вес рукоятки ОА не учитывать.
Вариант 14. Вес стержней ОА и ОВ не учитывать; пружина растянута.
Вариант 16. Вес стержней О1А и О2В не учитывать.
Вариант 18. Р – вес блока радиуса R3.
Вариант 19. Вес звена АВ не учитывать.
Вариант 24. Пружина сжата.
Вариант 25. Вес стержней АО и ВО не учитывать. Пружина растянута.
Вариант 26. Пружина растянута.
Применяя принцип возможных перемещений и пренебрегая силами сопротивления, определить величину, указанную в последнем столбце табл. 5.4.
Таблица 5.4
Продолжение табл. 5.4
Продолжение табл. 5.4
Продолжение табл. 5.4
Продолжение табл. 5.4
Продолжение табл. 5.4
Продолжение табл. 5.4
Продолжение табл. 5.4
Продолжение табл. 5.4
Окончание табл. 5.3
6.3.2. Пример выполнения курсового задания Д 6
При выполнении курсовых заданий Д 6, Д 7 необходимо учесть следующие замечания.

1. Если не все связи, наложенные на рассматриваемую механическую систему, являются идеальными, например, имеются шероховатые поверхности (неидеальные связи), то к активным нагрузкам следует добавить силы трения. Таким приёмом силы трения переносят в разряд активных сил и, следовательно, шероховатую поверхность можно рассматривать как идеальную связь (рис. 6.14).
Таким образом, при решении задачи рис. 6.14,а и рис. 6.14,б эквивалентны.
2. Если требуется определить какую-либо реакцию идеальной связи, то, применив аксиому связей, отбрасывают соответствующую связь и заменяют её реакцией связи. Таким образом, исходная связь заменяется другой связью, допускающей возможные перемещения. Тем самым искомая реакция переносится в разряд активных сил. Этот приём решения задач является черезвычайно эффективным, так как искомая реакция связи непосредственно определяется из уравнения, выражающего принцип возможных перемещений.
На рис. 6.15, 6.16 приведены некоторые варианты определения реакций внешних связей для механических систем.
В исходном положении (см. рис. 6.15) на механическую систему, состоящую из двух тел, в точке А наложена связь – жёсткая заделка. Снимем ограничение на перемещение тела 1 в горизонтальном направлении, сохранив остальные ограничения. Варианты такой замены показаны на рис. 6.15,б, 6.15,в.

При таких заменах тело 1 может совершить только поступательное движение, параллельное координатной оси ОХ. Если задать возможное перемещение δSA точке А механической системы, то её точки В и С получат возможные перемещения δSВ, δSС, зависящие от δSA.
При определении реактивного момента МА для механической системы, приведённой на рис 6.15, жёсткую заделку заменяют шарнирно-неподвижной опорой (см. рис. 6.16).
При такой замене тело 1 может совершать вращательное движение. Зададим этому телу возможное угловое перемещение δφ1. Точки В и С механической системы получат линейные возможные перемещения δSВ, δSС, зависящие от перемещения δφ1.
§
1. Изобразить рассматриваемую механическую систему на рисунке в соответствующем масштабе.
2. Приложить к механической системе активные нагрузки.
3. При наличии неидеальных связей добавить соответствующие реакции связей (например, силы трения).
4. Для определения реакции связи эту реакцию перенести в разряд активных сил путём замены существующей связи на связь, допускающую возможное перемещение в направлении, как правило, противоположном направлению определяемой реакции связи.
5. Задать возможное перемещение одной из точек механической системы и выразить возможные перемещения точек приложения сил в зависимости от заданного возможного перемещения.
6. Вычислить сумму работ активных сил на возможных перемещениях их точек приложения и приравнять эту сумму нулю.
7. Решив составленное уравнение, определить искомую величину.
Пример.
На рис. 6.17 изображена механическая система, находящаяся в равновесии. Определить модуль силы F, приложенной в точке А рычага 1.
Дано: G5 = 100 H; α = 30о; d1 = 1 м; b1 = 0,5 м; d3 = 0,8 м;
b3 = 0,5 м.
Решение.
Согласно рис. 6.17 механическая система, содержащая пять тел, имеет одну степень свободы. Наложенные на эту систему в точках С и К связи (шарнирно-неподвижные опоры) являются идеальными. На механическую систему, находящуюся в равновесии, действуют активные силы F и G5.

Зададим возможное угловое перемещение δφ1 телу 1, которое может совершать вращательное движение (рис. 6.18).
Модули возможных перемещений δSA , δSB точек А и В в зависимости от δφ1 определим по формулам:
δSA = δφ1·АС = δφ1·d1; δSB= δφ1·BC = δφ1·b1.
Решая совместно эти выражения, найдем зависимость
δSB= f(δSA) = δSA·b1/d1.
Из условия принадлежности точки D телу 3, которое получит возможное угловое перемещение δφ3, эта точка получит возможное перемещение δSD, перпендикулярное отрезку DK.
δSD = δφ3·DK = δφ3·d3.
Рассмотрим элементарное движение тела 2. Это тело совершает мгновенно поступательное движение, так как возможные перемещения δSB, δSD соответствующих точек этого тела одинаково направлены. Исходя из этого, имеем
δSD = δSB = δφ3·d3 = δSA·b1/d1.
Точка Е тела 3 получит возможное перемещение δSЕ, модуль δSЕ которого определим по формуле
δSЕ = δφ3·ЕK = δφ3·b3.
Выразим модуль возможного перемещения δSЕ точки Е сначала в зависимости от модуля возможного перемещения δSD точки D, а затем в зависимости от модуля возможного перемещения δSА точки А:
δSЕ = δSD·(b3/d3) = 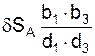 .
.
Так как участок нити EL и груз 5 совершают поступательные движения, то имеем
δSЕ = δSL = δSC5 = 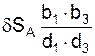 ,
,
где δSL, δSC5 – соответственно возможные перемещение точки L, принадлежащей нити 4 и центру С5 масс груза 5.
Запишем принцип возможных перемещений для рассматриваемой механической системы.
ΣFi·δSi·cos(Fi, δSi) = 0 = F·δSА·cos(α) – G5·δSC5 = 0.
Так как δSC5 = 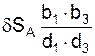 , то получим
, то получим
F·δSА·cos(α) – G5· 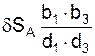 = 0.
= 0.
Решая последнее выражение, определим модуль силы F, при котором механическая система находится в равновесии.
6.3.3. Варианты курсового задания Д 7
«Применение принципа возможных перемещений
к определению реакций опор составной конструкции»
Применяя принцип возможных перемещений, определить реакции опор составной конструкции. Схемы конструкций и необходимые для решения данные приведены в табл. 5.5. На рисунках все размеры указаны в метрах.
Таблица 5.5
Продолжение табл. 5.5
Продолжение табл. 5.5
Продолжение табл. 5.5
Продолжение табл. 5.5
Продолжение табл. 5.5
Продолжение табл. 5.5
Продолжение табл. 5.5
Продолжение табл. 5.5
Окончание табл. 5.5
6.3.4. Пример выполнения курсового задания Д 7
Дано: конструкция, состоящая из двух тел, находится в равновесии под действием следующих нагрузок: Р1 = 2 кН; Р2 = 4 кН; М = 6 кН·м; q = 1 кН/м (рис. 6.19).
Применяя принцип возможных перемещений, определить реакции опор составной конструкции.
Решение.

Заменим равномерно распределённую нагрузку интенсивностью q сосредоточенной силой Q, приложенной в середине загруженного участка тела 1 (рис. 6.20). Модуль этой силы определим по формуле Q = q·2 = 1·2 = 2 кН.
Поскольку связи, наложенные на рассматриваемую механическую систему, являются идеальными, то для решения поставленной задачи правомерно применение принципа возможных перемещений.
Найдем горизонтальную составляющую ХА реакции в жёсткой заделке.
Согласно известным положениям статики жёсткая заделка накладывает три ограничения на перемещения тела в плоскости OXY (поступательные движения параллельно координатным осям и поворот в этой плоскости). Снимем ограничение на перемещение тела 1 только параллельно оси ОХ, сохраняя другие ограничения, и покажем на рисунке реакцию ХА. В результате этих действий реакция ХА переходит в разряд активных сил, а жёсткая заделка в точке А (см. рис. 6.19) заменяется кулисным камнем, к которому жёстко закреплено тело 1 составной конструкции. При такой замене составная конструкция становится подвижной.
Зададим возможное перемещение δSA точке А тела 1. Так как тело 1 может совершать только поступательное движение, то возможные перемещения всех точек этого тела геометрически равны:
δSA = δSP1 = δSQ = δSC,
где δSP1 – возможное перемещение точки приложения силы Р1; δSQ – возможное перемещение точки приложения силы Q; δSC – возможное перемещение точки С.
Так как точка С принадлежит и телу 2, то оно тоже будет подвижным. Для того, чтобы связь в точке В не разрушилась, эта точка получит возможное перемещение δSВ, параллельное опорной поверхности шарнирно-подвижной опоры. Поскольку возможные перемещения δSC, δSВ точек С и В тела 2 параллельны, то тело 2 совершает поступательное движение. Исходя из этого, имеем следующее равенство:
δSC = δSВ = δSР2,
где δSР2 – возможное перемещение точки приложения силы Р2.
Таким образом, возможные перемещения всех точек тел 1 и 2 геометрически равны:
δSA = δSP1 = δSQ = δSC = δSВ = δSР2.
Запишем уравнение, выражающее принцип возможных перемещений для рассматриваемого случая.
ΣFi·δSi·cos(Fi, δSi) = 0 = – XA·δSA P1·δSP1 – P2·cos(45о)·δSР2 = 0. (1)
Поскольку δSA = δSP1 = δSР2, то выражение (1) можно записать в следующем виде:
– XA·δSA P1·δSА – P2·cos(45о)·δSА = 0.
Решая последнее выражение относительно ХА, получим
XA = P1 – P2·cos(45о) = 2 – 4·0,707 = – 0,828 кН.
Найдем вертикальную составляющую YА реакции в жёсткой заделке.

Согласно известным положениям статики жёсткая заделка накладывает три ограничения на перемещения тела в плоскости OXY (поступательные движения параллельно координатным осям и поворот в этой плоскости). Снимем ограничение на перемещение тела 1 только параллельно оси ОY, сохраняя другие ограничения, и покажем на рисунке реакцию YА. В результате этих действий реакция YА переходит в разряд активных сил, а жёсткая заделка в точке А (рис. 6.21) заменяется кулисным камнем, к которому жёстко закреплено тело 1 составной конструкции. При такой замене составная конструкция становится подвижной.
Зададим возможное перемещение δSA точке А тела 1. Так как тело 1 может совершать только поступательное движение, то возможные перемещения всех точек этого тела геометрически равны:
δSA = δSP1 = δSQ = δSC,
где δSP1 – возможное перемещение точки приложения силы Р1; δSQ – возможное перемещение точки приложения силы Q; δSC – возможное перемещение точки С.
Так как точка С принадлежит и телу 2, то оно тоже будет подвижным. Для того, чтобы связь в точке В не разрушилась, эта точка должна получить возможное перемещение δSВ, параллельное опорной поверхности шарнирно-подвижной опоры. Поскольку возможные перемещения δSC, δSВ точек С и В тела 2 не параллельны, то тело 2 совершает плоскопараллельное движение. Очевидно, что мгновенный центр поворота тела 2 находится в точке В. Относительно оси, проходящей через точку В и перпендикулярной плоскости рис. 6.21, тело 2 повернётся на угол δφ2. Исходя из этого, имеем следующее равенство:
δSC = CB·δφ2 = 3·δφ2.
Следует заметить, что возможные перемещения δSC, δSP2 точки С и точки приложения силы Р2 перпендикулярны отрезкам, соединяющим эти точки с мгновенным центром поворота тела 2.
Принцип возможных перемещений выражается формулой
∑Fi·δSi·cos(Fi, δSi) = 0.
Так как величину угла между направлениями активной силы Р2 и возможным перемещением δSP2 точки приложения этой силы определять достаточно затруднительно, то элементарную работу приложенных к телу 2 сил определим через работу моментов сил относительно его мгновенного центра поворота, который расположен в точке В. С этой целью силу Р2 разложим на составляющие силы: P2·sin(45о) и P2·cos(45о).
Запишем уравнение, выражающее принцип возможных перемещений:
– YA·δSA Q·δSQ P2·sin(45о)·1,5·δφ2
P2·cos(45о)·3·δφ2 – M·δφ2 = 0. (2)
Так как δSA = δSQ = 3·δφ2, то выражение (2) можно преобразовать к следующему виду:
– YA·3·δφ2 Q·3·δφ2 P2·sin(45о)·1,5·δφ2
P2·cos(45о)·3·δφ2 – M·δφ2 = 0.
Решая последнее выражение относительно YA, получим
YA = Q 1 P2·sin(45о)·0,5 P2·cos(45о)·1 – M/3 =
= 2 1 4·0,707·0,5 4·0,707·1 – 6/3 = 4,242 кН.
Найдём реактивный момент МА в жёсткой заделке.
Жёсткая заделка накладывает три ограничения на перемещения тела в плоскости OXY (поступательные движения параллельно координатным осям и поворот в этой плоскости). Снимем ограничение на поворот тела 1 в плоскости ОХY, сохраняя другие ограничения, и покажем на рисунке реактивный момент МА. В результате этих действий реакция МА переходит в разряд активных нагрузок, а жёсткая заделка в точке А (рис. 6.22) заменяется шарнирно-неподвижной опорой. При такой замене составная конструкция становится подвижной. Тело 1 может совершать вращательное движение относительно оси, проходящей через точку А. Зададим телу 1 возможное угловое перемещение δφ1. Тогда точки приложения активных сил Р1, Q и точка С получат возможные перемещения δSP1, δSQ, δSC.
δSP1 = 1,5·δφ1; δSQ = ( 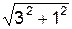 )·δφ1; δSC = CA·δφ1.
)·δφ1; δSC = CA·δφ1.
Следует отметить, что возможное перемещение δSC перпендикулярно отрезку, соединяющему точку С с осью вращения тела 1, проходящей через точку А.
Так как точка С принадлежит и телу 2, то оно тоже будет подвижным. Для того, чтобы связь в точке В не разрушилась, эта точка должна получить возможное перемещение δSВ, параллельное опорной поверхности шарнирно-подвижной опоры. Поскольку возможные перемещения δSC, δSВ точек С и В тела 2 не параллельны, то тело 2 совершает плоскопараллельное движение. Очевидно, что мгновенный центр поворота тела 2 находится в точке С2. Относительно оси, проходящей через точку С2 и перпендикулярную плоскости рис. 6.22, тело 2 повернётся на угол δφ2. Исходя из этого, имеем следующее равенство:
δSC = CС2·δφ2.
Так как точка С принадлежит и телу 1, и телу 2, то справедливо равенство
δSC = CA·δφ1 = CС2·δφ2.
Из рис. 6.22 нетрудно установить, что СА = СС2. Отсюда имеем
δφ1 = δφ2.
Возможные перемещения δSC, δSР2 точки С и точки приложения силы Р2 перпендикулярны отрезкам, соединяющим эти точки с мгновенным центром поворота тела 2.
В общем случае принцип возможных перемещений выражается формулой
∑Fi·δSi·cos(Fi, δSi) = 0.
Так как величину угла между направлениями активной силы Р2 и возможным перемещением δSP2 точки приложения этой силы определять достаточно затруднительно, то элементарную работу приложенных к телу 2 сил определим через работу моментов сил относительно его мгновенного центра поворота, который находится в точке С2. Как и ранее (см. рис. 6.21), силу Р2 разложим на составляющие силы: P2·sin(45о) и P2·cos(45о), параллельные координатным осям.
Запишем уравнение, выражающее принцип возможных перемещений.
– MA·δφ1 P1·1,5·δφ1 – Q·1·δφ1 –
– P2·sin(45о)·1,5·δφ2 – P2·cos(45о)·6·δφ2 M·δφ2 = 0. (3)
Поскольку δφ1 = δφ2, то выражение (3) можно преобразовать к виду
– MA·δφ1 P1·1,5·δφ1 – Q·1·δφ1 –
– P2·sin(45о)·1,5·δφ1 – P2·cos(45о)·6·δφ1 M·δφ1 = 0.
Решая это уравнение относительно МА, получим
MA = P1·1,5 – Q·1 – P2·sin(45о)·1,5 – P2·cos(45о)·6 M =
= 2·1,5 – 2·1 – 4·0,707·1,5 – 4·0,707·6 6 = – 14,210 кН·м.
Определим реакцию RB.
Шарнирно-подвижная опора в точке В накладывает только одно ограничение на перемещение тела 2 в пространстве. Снимем это ограничение на поступательное движение тела, параллельное оси ОY, и покажем на рис. 6.23 реакцию RB. Так как тело 1 неподвижно, то возможным перемещением тела 2 является его поворот относительно оси, проходящей через точку С на угол δφ2.
На рис. 6.23 показаны возможные перемещения δSВ, δSР2 точек приложения сил RB и Р2.
Составим уравнение, выражающее принцип возможных перемещений, при этом учтём, что работа силы при повороте тела равна произведению момента силы относительно мгновенного центра поворота на угол поворота тела.
P2·sin(45о)·1,5·δφ2 – P2·cos(45о)·3·δφ2 M·δφ2 – RB·δSB = 0. (4)
Так как δSB = 3·δφ2, то выражение (4) приводится к виду
P2·sin(45о)·1,5·δφ2 – P2·cos(45о)·3·δφ2 M·δφ2 – RB·3·δφ2 = 0.
Решая последнее выражение относительно RB, получим
RB = P2·sin(45о)·0,5 – P2·cos(45о)·1 M/3 =
= 4·0,707·0,5 – 4·0,707·1 6/3 = 0,586 кН.

Проведём проверку полученных результатов расчёта. Для этого рассмотрим равновесие составной конструкции под действием активных нагрузок Р1; Р2, М, Q и реакций внешних связей XA, YA, MA, RB (рис. 6.24).
Запишем уравнения равновесия для плоской произвольной системы сил и подставим в них определённые значения реакций внешних связей.
Σ  Σ
Σ  = 0 = XA – P1 P2·cos(45о) =
= 0 = XA – P1 P2·cos(45о) =
= – 0,828 – 2 4·0,707 = – 2,828 2,828 = 0;
Σ  Σ
Σ  = 0 = YA – P2·sin(45о) RB =
= 0 = YA – P2·sin(45о) RB =
= 4,242 – 2 – 4· 0,586 = 4,828 – 4,828 = 0;
ΣМА(  ) ΣМА(
) ΣМА( 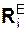 ) = 0 =
) = 0 =
= – MA P1·1,5 – Q·1 – P2·sin(45о)·4,5 – M RB·6 =
= – (–14,210) 2·1,5 – 2·1 – 4·0,707·4,5 – 6 0,586·6 =
= 20,728 – 20,728 = 0.
Проверка подтвердила правильность расчётов.
Вопросы и задания для самоконтроля
1. Сформулировать определение понятия «обобщённые координаты механической системы».
2. Что изучает аналитическая механика?
3. Сформулировать определение понятия «возможные перемещения несвободной механической системы».
4. Сформулировать определение понятия «связи».
5. Сформулировать определение понятия «геометрические связи».
6. Сформулировать определение понятия «стационарные связи».
7. Сформулировать определение понятия «уравнения связей».
8. Сформулировать определение понятия «дифференциальные связи».
9. Сформулировать определение понятия «голономные связи».
10. Сформулировать определение понятия «неголономные связи».
11. Сформулировать определение понятия «нестационарные связи».
12. Сформулировать определение понятия «двусторонние (удерживающие) связи».
13. Сформулировать определение понятия «односторонние (неудерживающие) связи».
14. Сформулировать определение понятия «голономная система».
15. Сформулировать определение понятия «неголономная система».
16. Сформулировать определение понятия «возможное перемещение системы».
17. Сформулировать определение понятия «возможная (элементарная) работа силы».
18. Записать формулу для определения возможной работы силы.
19. Записать формулу для определения возможной работы сил, приложенных к механической системе.
20. Сформулировать определение понятия «идеальные связи».
21. Сформулировать принцип возможных перемещений.
22. Записать формулу, выражающую принцип возможных перемещений, в векторной форме.
23. Записать формулу, выражающую принцип возможных перемещений, в координатной форме.
24. Записать формулу, выражающую принцип возможных скоростей (принцип возможных мощностей).
§
6.4.1. Общее уравнение динамики механической системы
Принцип возможных перемещений, дающий общий метод решения задач статики, можно применить и к решению задач динамики, если его дополнить принципом Даламбера.
Рассмотрим движение несвободной неизменяемой механической системы, на которую наложены идеальные связи, в инерциальной системе отсчёта OXYZ (рис. 6.25).
Согласно принципу Даламбера i-я точка механической системы совершает движение под действием активной силы  , реакции
, реакции 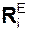 внешней связи, реакции
внешней связи, реакции 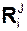 внутренней связи и силы инерции Фi. Этот принцип выражается формулой
внутренней связи и силы инерции Фi. Этот принцип выражается формулой

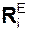
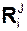 Фi = 0.
Фi = 0.

Пусть точка Сi механической системы получит возможное перемещение δSСi. Очевидно, что элементарная работа δА сил, приложенных к точке, равна нулю.
δА = ( 
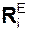
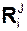 Фi)·δSСi = 0.
Фi)·δSСi = 0.
Просуммируем последние выражения и получим
Σ  ·δSСi Σ
·δSСi Σ 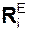 ·δSСi Σ
·δSСi Σ 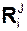 ·δSСi ΣФi·δSСi = 0.
·δSСi ΣФi·δSСi = 0.
Для движущейся механической системы сумма работ активных сил, реакций внешних связей, внутренних сил и сил инерции, приложенных к её точкам, на любых возможных перемещениях этой системы равна нулю.
Поскольку на механическую систему наложены идеальные связи, то сумма работ реакций этих связей равна нулю.
Σ 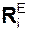 ·δSСi = 0.
·δSСi = 0.
Так как рассматривается неизменяемая механическая система, то сумма работ реакций внутренних связей также равна нулю.
Σ 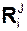 ·δSСi = 0.
·δSСi = 0.
Исходя из того, что Σ 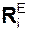 ·δSСi = 0 и Σ
·δSСi = 0 и Σ 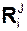 ·δSСi = 0, получим
·δSСi = 0, получим
Σ  ·δSСi ΣФi·δSСi = 0.
·δSСi ΣФi·δSСi = 0.
Последнее уравнение называют общим уравнением динамики.
В любой момент времени работа активных сил и сил инерции материальных точек несвободной механической системы с идеальными связями на её любом возможном перемещении равна нулю.
Общее уравнение динамики (Σ  ·δSСi ΣФi·δSСi = 0) можно преобразовать к следующим видам:
·δSСi ΣФi·δSСi = 0) можно преобразовать к следующим видам:
Σ(  Фi)·δSСi = 0;
Фi)·δSСi = 0;
Σ 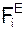 ·δSСi·cos(
·δSСi·cos(  , δSСi) ΣФi·δSСi·cos(Фi, δSСi) = 0;
, δSСi) ΣФi·δSСi·cos(Фi, δSСi) = 0;
Σ(  ·δSiОХ
·δSiОХ  ·δSiOY
·δSiOY  ·δSiOZ)
·δSiOZ)
Σ(ФiOX·δSiOX ФiOY·δSiOY ФiOZ·δSiOZ) = 0;
Σ(  ·δSiOX
·δSiOX  ·δSiOY
·δSiOY  ·δSiOZ)
·δSiOZ)
Σ(– m· 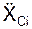 ·δSiOX – m·
·δSiOX – m· 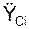 ·δSiOY – m·
·δSiOY – m· 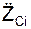 ·δSiOZ) = 0,
·δSiOZ) = 0,
где  ,
,  ,
,  – проекции активных сил на координатные оси; ФiOX, ФiOY, ФiOZ – проекции сил инерции на координатные оси; δSiOX, δSiOY, δSiOZ – проекции возможных перемещений точек приложения сил на координатные оси,
– проекции активных сил на координатные оси; ФiOX, ФiOY, ФiOZ – проекции сил инерции на координатные оси; δSiOX, δSiOY, δSiOZ – проекции возможных перемещений точек приложения сил на координатные оси, 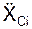 ,
, 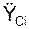 ,
, 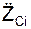 – проекции ускорений материальных точек механической системы на координатные оси.
– проекции ускорений материальных точек механической системы на координатные оси.
Общее уравнение динамики позволяет составить дифференциальные уравнения движения любой механической системы.
Если среди связей системы имеются односторонние связи, то для применения общего уравнения динамики необходимо, чтобы возможные перемещения системы не разрушали эти связи, а обеспечивали их функциональное назначение.
Для закрепления изложенного теоретического материала рекомендуется выполнить курсовое задание Д 8.
6.4.2. Варианты курсового задания Д 8
«Применение общего уравнения
динамики к исследованию движения механической
системы с одной степенью свободы»
Для заданной механической системы определить ускорения центров масс грузов 1. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя.
Варианты механических систем и необходимые для решения данные приведены в табл. 5.6.
Блоки и катки, для которых радиусы инерции в табл. 5.6 не указаны, считать сплошными однородными цилиндрами.
Примечания:
Радиусы инерции даны относительно центральных осей, перпендикулярных плоскости чертежа.
Коэффициенты трения принимать одинаковыми при скольжении тел по плоскостям.
Таблица 5.6
Продолжение табл. 5.6
Продолжение табл. 5.6
Продолжение табл. 5.6
Продолжение табл. 5.6
Продолжение табл. 5.6
Продолжение табл. 5.6
Продолжение табл. 5.6
Продолжение табл. 5.6
Окончание табл. 5.6
6.4.3. Пример выполнения курсового задания Д 8

Для заданной механической системы (рис. 6.26) определить ускорение груза 1 при его опускании.
Дано: G1 = 8G; G2 = 4G; G3 = 2G; P = G; f3 = 0,1; iC2X2 = 0,1 м; f4 = 0,1; α = 30o; b = 0,5 м; d = 0,4 м; r2 = 0,2 м; R2 = 0,5 м, где G1, G2, G3 – вес соответствующих тел механической системы; f3 – коэффициент трения скольжения тела 3 при его движении по шероховатой поверхности; f4 – коэффициент трения скольжения между телами 2 и 4; iC2X2 – радиус инерции тела 2 относительно оси, проходящей через его центр масс; α, b, d, r2, R2 – геометрические параметры. Механическая система начинает движение из состояния покоя.
Решение.
Рассмотрим движение механической системы, состоящей из тел 1, 2, 3 (рис. 6.27), предположив, что груз 1 опускается ускоренно.
Согласно общему уравнению динамики механическая система совершает движение под действием активных сил: G1, G2, G3 – силы тяжести тел 1, 2, 3; F3 – сила трения при движении груза 3 по шероховатой поверхности; F4-2 – сила трения при скольжении цилиндрической поверхности тела 2 по тормозной колодке тела 4 и инерционных нагрузок: Ф1, Ф3 – силы инерции тел 1, 3; 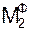 – момент сил инерции при вращении тела 2 относительно оси С2Х2.
– момент сил инерции при вращении тела 2 относительно оси С2Х2.
Как это отмечалось ранее, при наличии неидеальных связей, наложенных на механическую систему, эти связи необходимо преобразовать в идеальные путём переноса сил трения в разряд активных сил.
Для определения силы трения F4-2 механическую систему, показанную на рис. 6.26, расчленим по внутренней связи и рассмотрим равновесие рычага 4 (рис. 6.28).
На тело 4 действуют: активная сила Р; реакции YA, ZA внешней связи в точке А (шарнирно-неподвижная опора); реакции N2-4, F2-4 внутренней связи. Направления сил N2-4, F2-4 показывают, как тело 2 действует на тело 4. Составим уравнение равновесия.
ΣMA( 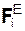 ) ΣMA(
) ΣMA( 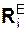 ) = N2-4·b – P·(b d) = 0.
) = N2-4·b – P·(b d) = 0.
Из этого уравнения определим модуль нормальной реакции
N2-4 = P·(b d)/b = G·(b d)/b.
Согласно закону сухого трения (закону Кулона) сила трения F2-4 связана с нормальной реакцией N2-4 соотношением
F2-4 = f4·N2-4 = f4·G·(b d)/b.
По известному закону динамики (закон равенства действия и противодействия) имеем
F4-2 = F2-4 = f4·G·d/b.
Таким образом, сила F4-2 трения, приложенная к телу 2 со стороны тела 4 (см. рис. 6.27), определена.

Для определения силы F3 трения рассмотрим поступательное движение груза 3 (рис. 6.29) в инерциальной системе отсчёта O3Y3X3. Используя известные положения динамики, примем груз 3 за материальную точку.
На рис. 6.29 использованы условные обозначения: N3 – нормальная реакция шероховатой поверхности; VС3, aС3 – соответственно скорость и ускорение центра масс тела 3.
Составим дифференциальное уравнение поступательного движения тела 3.
m· 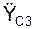 = – G3·cos(α) N3,
= – G3·cos(α) N3,
где 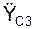 – проекция ускорения aС3 на координатную ось O3Y3.
– проекция ускорения aС3 на координатную ось O3Y3.
Так как 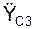 = 0, то получим
= 0, то получим
N3 = G3·cos(α).
Тогда имеем
F3 = f3·N3 = f3·G3·cos(α) = f3·2·G·cos(α).
Таким образом, сила трения F3 определена.
Вернёмся к рис. 6.27. Зададим возможное перемещение δSС1 центру масс тела 1. При этом тело 2 получит возможное угловое перемещение δφ2 = δSС1/R2, а центр С3 масс тела 3 получит возможное линейное перемещение, модуль которого δSС3 = δSС1·(r2/R2). Двойным дифференцированием по времени возможных перемещений δφ2, δSС3 определим угловое ускорение 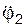 тела 2 и модуль aС3 ускорения центра масс тела 3.
тела 2 и модуль aС3 ускорения центра масс тела 3.
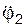 = aС1/R2; aС3 = aС1·(r2/R2).
= aС1/R2; aС3 = aС1·(r2/R2).
К рассматриваемой механической системе приложим активные силы G1, G2, G3, F3, F4-2 и инерционные нагрузки Ф1, Ф2, 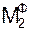 .
.
Модули сил инерции Ф1, Ф3 и момента 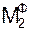 сил инерции определяют по формулам:
сил инерции определяют по формулам:
Ф1 = m1·aС1 = (G1/g)·aС1 = (8·G/g)·aС1;
Ф3 = m1 ·aС3 = (G3/g)·aС3 = (2·G/g)·aС1·(r2/R2);
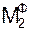 = JС2Х2·
= JС2Х2· 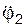 = m2·(iС2Х2)2·
= m2·(iС2Х2)2· 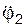 = (G2/g)·(iС2Х2)2·
= (G2/g)·(iС2Х2)2· 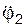 =
=
= (4·G/g)·(iС2Х2)2·(aС1/R2).
Запишем общее уравнение динамики для рассматриваемой механической системы:
Σ  ·δSСi·cos(
·δSСi·cos(  , δSСi) ΣФi·δSСi·cos(Фi, δSСi) = 0.
, δSСi) ΣФi·δSСi·cos(Фi, δSСi) = 0.
Определим первое слагаемое правой части этого уравнения.
Σ  ·δSСi·cos(
·δSСi·cos(  , δSСi) =
, δSСi) =
= G1·δSС1 – F4-2·δSС1 – G3·δSС3·sin(α) – F3·δSС3 =
= 8·G·δSС1 – f4·G·((b d)/b)·δSС1 – 2·G·δSС1·(r2/R2)·sin(α) –
– f3·2·G·cos(α)·δSС1·(r2/R2) =
= G·(8 – f4·((b d)/b) – 2·(r2/R2)·sin(α) – f3·2·G·cos(α)·(r2/R2))·δSС1.
Определим второе слагаемое правой части общего уравнения динамики:
ΣФi·δSСi·cos(Фi, δSCi) = – Ф1·δSС1 – 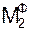 ·δφ2 – Ф3·δSС3 =
·δφ2 – Ф3·δSС3 =
= – (8·G/g)·aС1·δSС1 – (4·G/g)·(iС2Х2)2·(aС1/R2)·(δSС1/R2) –
– (2·G/g)·aС1·(r2/R2)·δSС1·(r2/R2) =
= – (G/g)·(8 4·(iС2Х2/R2)2 2·(r2/R2)2)·aС1·δSС1.
Внося эти слагаемые в общее уравнение динамики, получим
G·(8 – f4·((b d)/b) – 2·(r2/R2)·sin(α) – f3·2·G·cos(α)·(r2/R2))·δSС1 –
– (G/g)·(8 4·(iС2Х2/R2)2 2·(r2/R2)2)·aС1·δSС1 = 0.
Отсюда определим модуль aС1 ускорения центра масс груза 1:
aC1 = g·(8 – f4·((b d)/b) – 2·(r2/R2)·sin(α) – f3·2·cos(α)·(r2/R2))/
/(8 4·(iС2Х2/R2)2 2·(r2/R2)2) =
= 9,81·(8 – 0,1·((0,5 0,4)/0,5) – 2·(0,2/0,5)·0,5 –
– 0,1·2·0,866·(0,2/0,5))/
/(8 4·(0,1/0,5)2 2·(0,2/0,5)2) = 9,584 м/с2.
Таким образом, ответ на вопрос (aС1 =?), поставленный в курсовом задании Д 8, получен.
Вопросы и задания для самоконтроля
1. Записать формулу, выражающую общее уравнение динамики, в векторной форме.
2. Записать формулу, выражающую общее уравнение динамики, в скалярной форме.
3. Записать формулу, выражающую общее уравнение динамики, в координатной форме.
§
Уравнения Лагранжа второго рода – дифференциальные уравнения движения механической системы в обобщённых координатах.
Для механической системы с n степенями свободы эти уравнения имеют вид
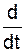 (∂TS/∂
(∂TS/∂ 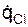 ) – ∂TS/∂qCi = Qqci, i = 1, …, n,
) – ∂TS/∂qCi = Qqci, i = 1, …, n,
где ТS – кинетическая энергия механической системы; qCi – обобщённая координата; 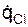 – обобщённая скорость; Qqci – обобщённая сила по обобщённой координате qCi.
– обобщённая скорость; Qqci – обобщённая сила по обобщённой координате qCi.
Число уравнений Лагранжа второго рада равно числу степеней свободы рассматриваемой механической системы.
Используя рис 6.30, поясним понятия «обобщённая скорость», «обобщённая сила».

На рис. 6.30 приняты условные обозначения:  – активная сила, приложенная к точке механической системы; δqCi – приращение обобщённой координаты qCi (возможное перемещение i-й точки системы);
– активная сила, приложенная к точке механической системы; δqCi – приращение обобщённой координаты qCi (возможное перемещение i-й точки системы); 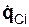 – обобщённая скорость i-й точки механической системы.
– обобщённая скорость i-й точки механической системы.
Обобщённая скорость – производная по времени от обобщённой координаты.
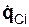 = dqCi/dt.
= dqCi/dt.
Определим возможную элементарную работу δАS(  ) активных сил
) активных сил  , приложенных к точкам механической системы при задании какой-либо её точке возможного перемещения δqCi.
, приложенных к точкам механической системы при задании какой-либо её точке возможного перемещения δqCi.
δАS(  ) = Σ
) = Σ 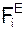 ·δqCi·cos(
·δqCi·cos(  , δqCi).
, δqCi).
Обобщенная сила Qqci по обобщенной координате qCi – величина, равная отношению возможной элементарной работы δАS активных сил  , приложенных к точкам механической системы, к модулю δqСi приращения обобщённой координаты qCi.
, приложенных к точкам механической системы, к модулю δqСi приращения обобщённой координаты qCi.
Qqi = δAS(  )/δqCi.
)/δqCi.
Формулировка уравнения Лагранжа второго рода.
Разность полной производной по времени от частной производной кинетической энергии по обобщенной скорости и частной производной от кинетической энергии по обобщенной координате равна обобщенной силе.
Уравнения Лагранжа второго рода используют в качестве универсального метода составления дифференциальных уравнений движения механических систем любой степени сложности. Преимущество этого метода по сравнению с применяемыми ранее общими теоремами динамики заключается в том, что в уравнениях Лагранжа второго рода используются только активные силы. Это намного упрощает решение задач динамики механических систем.
Согласно учебной программе выполнение курсового задания на применение уравнений Лагранжа второго рода к исследованию движения механических систем не предусмотрено. Тем не менее для развития общего кругозора студента приведём пример решения такого типа задач.
Пример.
Однородный барабан 1 массой m1 и радиусом R1 приводится во вращение активным моментом М. На барабан наматывается невесомый трос, перекинутый через невесомый блок 2. К свободному концу троса прикреплён груз 3 массой m3 (рис. 6.31).
Механическая система начинает двигаться из состояния покоя. Составить дифференциальное уравнение вращательного движения барабана.
Дано: m1 = 20 кг; R1 = 0,2 м; m3 = 10 кг; М = 200 Н·м.
Решение.

Механическая система имеет одну степень свободы. Примем за обобщённую координату q угол φ1 поворота тела 1 (рис. 6.32).
Запишем уравнение Лагранжа второго рода для рассматриваемой механической системы.
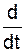 (∂TS/∂
(∂TS/∂  ) – ∂TS/∂φ1 = Qφ1,
) – ∂TS/∂φ1 = Qφ1,
где ТS – кинетическая энергия механической системы; Qφ1 – обобщённая сила по обобщённой координате φ1;  – обобщённая скорость.
– обобщённая скорость.
Зададим приращение δφ1 обобщённой координате φ1. Тогда центр масс тела 3 получит возможное перемещение
δSС3 = δφ1·R1.
Кинетическая энергия механической системы равна
ТS = Т1 Т3,
где Т1 – кинетическая энергия барабана 1; Т3 – кинетическая энергия груза 3.
Тело 1 совершает вращательное движение относительно оси С1Х1. Его кинетическую энергию определим по формуле
T1 = 0,5·JC1X1·(  )2 = 0,5·(m1·(R1)2/2)·(
)2 = 0,5·(m1·(R1)2/2)·(  )2 = 0,25·m1·(R1)2·(
)2 = 0,25·m1·(R1)2·(  )2.
)2.
Согласно рис. 6.32 тело 3 совершает поступательное движение. Исходя из этого утверждения, его кинетическую энергию определим по формуле
T3 = 0,5·m3·(VC3)2 = 0,5·m3·(  ·R1)2.
·R1)2.
В последней формуле символом VC3 обозначена скорость центра масс тела 3.
Кинетическая энергия механической системы
ТS = 0,25·m1·(R1)2·(  )2 0,5·m3·(
)2 0,5·m3·(  ·R1)2 =
·R1)2 =
= (0,25·m1 0,5·m3)·(  ·R1)2.
·R1)2.
Определим частную производную от кинетической энергии механической системы по обобщённой скорости  .
.
∂TS/∂  = 2·(0,25·m1 0,5·m3)·(R1)2·
= 2·(0,25·m1 0,5·m3)·(R1)2· 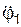 .
.
Тогда
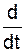 (∂TS/∂
(∂TS/∂  ) = (0,5·m1 m3)·(R1)2·
) = (0,5·m1 m3)·(R1)2· 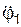 .
.
Так как кинетическая энергия системы не зависит от обобщённой координаты φ1, то соответственно её частная производная ∂TS/∂φ1 равна нулю (∂TS/∂φ1 = 0).
Тогда левая часть уравнения Лагранжа вторго рода равна
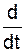 (∂TS/∂
(∂TS/∂  ) – ∂TS/∂φ1 = (0,5·m1 m3)·(R1)2·
) – ∂TS/∂φ1 = (0,5·m1 m3)·(R1)2· 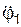 .
.
Определим элементарную работу δАS(  ) сил, приложенных к механической системе на её возможном перемещении.
) сил, приложенных к механической системе на её возможном перемещении.
δАS(  ) = M·δφ1 – G3·δSC3 = M·δφ1 – m3·g·δφ1·R1 =
) = M·δφ1 – G3·δSC3 = M·δφ1 – m3·g·δφ1·R1 =
= (M – m3·g·R1)·δφ1.
Согласно определению обобщённая сила Qφ1 по обобщённой координате φ1 равна
Qφ1 = δАS/ δφ1 = M – m3·g·R1.
Уравнение Лагранжа второго рода для рассматриваемой механической системы принимает вид
(0,5·m1 m3)·(R1)2· 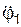 = M – m3·g·R1.
= M – m3·g·R1.
Решая это уравнение относительно углового ускорения 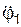 , получим
, получим
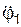 =
= 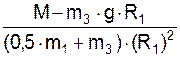 =
=
= 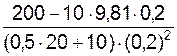 = 17,344 м/с2.
= 17,344 м/с2.
Дважды интегрируя эти дифференциальные уравнения и определив постоянные интегрирования, получим:
 = 17,344·t; φ1 = 8,672·t2.
= 17,344·t; φ1 = 8,672·t2.
§
Гироскопом называют симметричное твёрдое тело, угловая скорость  вращения которого относительно оси симметрии значительно превосходит по модулю угловую скорость
вращения которого относительно оси симметрии значительно превосходит по модулю угловую скорость  вращения оси симметрии.
вращения оси симметрии.
I  I = ω1 >> I
I = ω1 >> I  I = ω2,
I = ω2,
где ω1, ω2 – модули угловых скоростей  ,
,  .
.
В современных гироскопических приборах частота n1 вращения относительно оси симметрии (оси гироскопа) достигает значений 40000 – 50000 об/мин (ω1 = 4200 – 5200 рад/с), а частота n2 вращения оси симметрии равна одному обороту за 2 – 3 минуты (n2 = 3, 14 – 4, 73 об/мин) и даже за 20 минут (n2 = 0,314 об/мин) для гирокомпасов.

Рассмотрим случай, когда гироскоп движется в инерциальной системе отсчёта O2X2Y2Z2 около неподвижной точки О2 (рис. 7.1).
На рис. 7.1 приняты условные обозначения: O2X2Y2Z2 – инерциальная система отсчёта (ИСО); O1X1Y1Z1 – подвижная система отсчёта (ПСО);  – вектор угловой скорости
– вектор угловой скорости  вращения гироскопа относительно оси симметрии (ось симметрии гироскопа совпадает с осью O1Z1 подвижной системы отсчёта);
вращения гироскопа относительно оси симметрии (ось симметрии гироскопа совпадает с осью O1Z1 подвижной системы отсчёта); 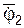 – вектор угловой скорости
– вектор угловой скорости  вращения оси O1Z1 симметрии гироскопа относительно оси O2Z2 инерциальной системы отсчёта O2X2Y2Z2; θ – угол наклона оси O1Z1 симметрии к оси O2Z2 инерциальной системы отсчёта (угол нутации); LO(
вращения оси O1Z1 симметрии гироскопа относительно оси O2Z2 инерциальной системы отсчёта O2X2Y2Z2; θ – угол наклона оси O1Z1 симметрии к оси O2Z2 инерциальной системы отсчёта (угол нутации); LO(  ) – кинетический момент гироскопа относительно точки О при его вращении вокруг оси симметрии O1Z1 с угловой скоростью
) – кинетический момент гироскопа относительно точки О при его вращении вокруг оси симметрии O1Z1 с угловой скоростью  ; LO(
; LO( 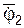 ) – кинетический момент гироскопа относительно точки О при его вращении вокруг оси O2Z2 инерциальной системы отсчёта O2X2Y2Z2 с угловой скоростью
) – кинетический момент гироскопа относительно точки О при его вращении вокруг оси O2Z2 инерциальной системы отсчёта O2X2Y2Z2 с угловой скоростью  ; LO – кинетический момент гироскопа относительно точки О при его вращении с угловой скоростью
; LO – кинетический момент гироскопа относительно точки О при его вращении с угловой скоростью  вокруг мгновенной оси вращения OZ3;
вокруг мгновенной оси вращения OZ3;  – вектор угловой скорости
– вектор угловой скорости  вращения гироскопа относительно мгновенной оси вращения OZ3.
вращения гироскопа относительно мгновенной оси вращения OZ3.
Начала О1 подвижной системы отсчёта O1X1Y1Z1 и О2 инерциальной системы отсчёта O2X2Y2Z2 помещены в точку О.
Гироскоп вращается с угловой скоростью  относительно оси O1Z1 симметрии, которая в свою очередь вращается с угловой скоростью
относительно оси O1Z1 симметрии, которая в свою очередь вращается с угловой скоростью  относительно оси O2Z2 инерциальной системы отсчёта O2X2Y2Z2.
относительно оси O2Z2 инерциальной системы отсчёта O2X2Y2Z2.
Вектор  абсолютной угловой скорости гироскопа определяют по формуле
абсолютной угловой скорости гироскопа определяют по формуле  =
= 
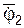 . При этом вектор
. При этом вектор  лежит на мгновенной оси OZ3 вращения гироскопа.
лежит на мгновенной оси OZ3 вращения гироскопа.
Кинетический момент LO гироскопа относительно точки О равен
LO = LO(  ) LO(
) LO( 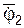 ).
).
В развёрнутом виде последняя формула выглядит следующим образом:
LO = JO1Z1·(  ) JO2Z2·(
) JO2Z2·( 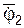 ),
),
где JO1Z1, JO2Z2 – моменты инерции гироскопа относительно осей O1Z1, O2Z2.
Так как I  I << I
I << I  I, то величина угла θ очень мала (в современных приборах она составляет доли секунды). Тогда с достаточной для инженерной практики точностью можно считать, что
I, то величина угла θ очень мала (в современных приборах она составляет доли секунды). Тогда с достаточной для инженерной практики точностью можно считать, что
LO( 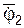 ) = JO2Z2·(
) = JO2Z2·( 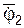 ) = 0.
) = 0.
С учётом этого допущения имеем
LO = JO1Z1·(  ).
).
Из последнего выражения следует, что вектор LO кинетического момента гироскопа относительно точки О совпадает с осью симметрии гироскопа. Исходя из этого утверждения, рис. 7.1 можно преобразовать к следующему виду (рис. 7.2).
На таком допущении основана приближённая (элементарная) теория гироскопов.
При решении задач с помощью приближённой теории гироскопов удобно пользоваться теоремой Резаля, которая выражается формулой
dLO/dt = U = Σ MO(FiE) Σ MO(RiE) =  ,
,
где LO – кинетический момент гироскопа относительно точки О; U – скорость конца вектора LO в инерциальной системе отсчёта; Σ MO(FiE), Σ MO(RiE) – геометрические суммы моментов активных сил FiE и реакций RiE внешней связи относительно точки О;  – главный момент внешних сил, приложенных к гироскопу, относительно точки О.
– главный момент внешних сил, приложенных к гироскопу, относительно точки О.
Скорость U конца вектора LO кинетического момента гироскопа относительно точки О направлена так же , как и вектор  главного момента внешних сил , приложенных к гироскопу, относительно той же точки.
главного момента внешних сил , приложенных к гироскопу, относительно той же точки.
Использование теоремы Резаля позволяет решать следующие задачи: 1) по известным активным силам FiE и реакциям RiE внешней связи определяют направление движения оси симметрии гироскопа; 2) по известному закону движения оси гироскопа определяют главный момент внешних сил  .
.
Пример 1.
Гироскоп совершает быстрое вращение относительно вертикальной оси OZ симметрии, имея неподвижную точку О (рис. 7.3).
Определить направление движения оси симметрии гироскопа, если к ней приложена активная сила FiE, которая параллельна плоскости OYZ.
Решение.
Приложим к гироскопу активную силу FiE, силу тяжести G и реакции XO, YO, ZO внешней связи в точке О (рис. 7.4).
Определим главный момент  внешних сил относительно точки О.
внешних сил относительно точки О.
 = Σ MO(FiE) Σ MO(G) Σ MO(XO) Σ MO(YO) Σ MO(ZO).
= Σ MO(FiE) Σ MO(G) Σ MO(XO) Σ MO(YO) Σ MO(ZO).
Так как Σ MO(G) = 0, Σ MO(XO) = 0; Σ MO(YO) = 0, Σ MO(ZO) = 0, то имеем
 = Σ MO(FiE).
= Σ MO(FiE).
Главный момент  внешних сил относительно точки О приложен в этой точке и направлен по оси ОХ в сторону увеличения координаты Х (напомним, что момент силы относительно точки направляется перпендикулярно плоскости, проходящей через силу и точку так, что с его конца видно, что сила стремится повернуть тело вокруг точки против хода часовой стрелки).
внешних сил относительно точки О приложен в этой точке и направлен по оси ОХ в сторону увеличения координаты Х (напомним, что момент силы относительно точки направляется перпендикулярно плоскости, проходящей через силу и точку так, что с его конца видно, что сила стремится повернуть тело вокруг точки против хода часовой стрелки).
Кинетический момент LO = JOZ·  гироскопа относительно точки О направлен в сторону вектора
гироскопа относительно точки О направлен в сторону вектора  угловой скорости вращения. Конец вектора LO обозначим точкой D.
угловой скорости вращения. Конец вектора LO обозначим точкой D.
Применив теорему Резаля U =  , направляем вектор U скорости точки D параллельно вектору
, направляем вектор U скорости точки D параллельно вектору  .
.
Таким образом, ось OZ симметрии гироскопа будет перемещаться в плоскости OXZ, которая перпендикулярна направлению активной силы FiE.
Пример 2.
Определить движение тяжёлого гироскопа, ось которого составляет угол θ с вертикалью, если:  – угловая скорость вращения относительно оси O1Z1 симметрии; JO1Z1 – момент инерции гироскопа относительно оси симметрии; b = OC – расстояние от центра тяжести С до точки О опоры (рис. 7.5).
– угловая скорость вращения относительно оси O1Z1 симметрии; JO1Z1 – момент инерции гироскопа относительно оси симметрии; b = OC – расстояние от центра тяжести С до точки О опоры (рис. 7.5).
Рассмотрим движение гироскопа в инерциальной системе отсчёта OXYZ (рис. 7.6).
Приложим к гироскопу активную силу G (силу тяжести) и реакции XO, YO, ZO внешней связи в точке О. Модуль 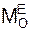 главного момента
главного момента  внешних сил, приложенных к гироскопу, равен
внешних сил, приложенных к гироскопу, равен
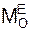 = G·OC·sin(θ).
= G·OC·sin(θ).
Вектор  главного момента внешних сил направлен по оси OY в сторону увеличения координаты Y.
главного момента внешних сил направлен по оси OY в сторону увеличения координаты Y.
Кинетический момент LO гироскопа относительно точки О направлен по оси симметрии в сторону вектора  угловой скорости и равен по модулю
угловой скорости и равен по модулю
LO = JO1Z1·ω,
где ω = I  I – модуль вектора угловой скорости
I – модуль вектора угловой скорости  .
.
Обозначим точкой D конец вектора LO. Согласно теореме Резаля, U =  . Поэтому U – скорость точки D направлена перпендикулярно к оси симметрии (параллельна оси ОХ) в сторону увеличения координаты Х. Модуль U скорости U равен
. Поэтому U – скорость точки D направлена перпендикулярно к оси симметрии (параллельна оси ОХ) в сторону увеличения координаты Х. Модуль U скорости U равен
U = 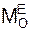 = G·OC·sin(θ) = const.
= G·OC·sin(θ) = const.
Таким образом, точка D имеет постоянную по модулю скорость U, направленную перпендикулярно к вертикальной плоскости, содержащей ось симметрии гироскопа. При этом ось гироскопа описывает боковую поверхность кругового конуса, поворачиваясь относительно вертикальной оси OZ с угловой скоростью  . Это движение называют регулярной прецессией оси гироскопа.
. Это движение называют регулярной прецессией оси гироскопа.
Вычислим модуль ω1 угловой скорости  регулярной прецессии.
регулярной прецессии.
ω1 = I  I = U/(DA) =
I = U/(DA) = 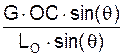 =
= 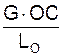 =
= 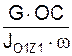 .
.
Окончательно имеем
ω1 = 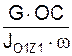 .
.
Чем меньше модуль ω угловой скорости  вращения гироскопа относительно его оси симметрии, тем больше модуль ω1 угловой скорости
вращения гироскопа относительно его оси симметрии, тем больше модуль ω1 угловой скорости  прецессии (от величины угла θ угловая скорость прецессии не зависит).
прецессии (от величины угла θ угловая скорость прецессии не зависит).
Задачи на определение движения оси гироскопа с помощью приближённой теории рекомендуется решать по следующему алгоритму.
1. Проверить, имеет ли гироскоп три степени свободы.
2. Выбрать систему координат.
3. Изобразить на рисунке внешние силы, приложенные к гироскопу.
4. Определить главный момент  внешних сил относительно неподвижной точки О.
внешних сил относительно неподвижной точки О.
5. Найти кинетический момент LO гироскопа относительно неподвижной точки О.
6. Применив теорему Резаля U =  , определить движения оси гироскопа.
, определить движения оси гироскопа.
В экзаменационных задачах, как правило, требуется определить ω, JO1Z1, ОС. Эти величины определяют по формулам:
ω1 = 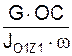 ;
;
JO1Z1 = 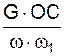 ;
;
ОС = 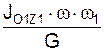 .
.
Пример 3.
На рис. 7.7 приведена схема гироскопа в кардановом подвесе. Конструктивная схема содержит корпус 1, уравновешенный массивный круглый цилиндр, горизонтальную 3 и вертикальную рамки.
Тело 2 вращается с угловой скоростью  в подшипниках горизонтальной рамки 3 относительно оси ОХ. Рамка 3 может поворачиваться в подшипниках рамки 4 относительно оси OY. В свою очередь рамка 4 может поворачиваться в подшипниках корпуса 1 гироскопа относительно оси OZ. Координатные оси OX, OY, OZ пересекаются в центре масс механической системы, состоящей из тел 2, 3, 4.
в подшипниках горизонтальной рамки 3 относительно оси ОХ. Рамка 3 может поворачиваться в подшипниках рамки 4 относительно оси OY. В свою очередь рамка 4 может поворачиваться в подшипниках корпуса 1 гироскопа относительно оси OZ. Координатные оси OX, OY, OZ пересекаются в центре масс механической системы, состоящей из тел 2, 3, 4.
Если точки О и С совпадают, то такой гироскоп называют астатическим (уравновешенным), в противном случае – тяжёлым.
Определить изменение положения оси ОХ вращения тела 2, пренебрегая трением в подшипниках.
Решение.
Гироскоп в кардановом подвесе имеет три степени свободы, так как его положение определяется тремя независимыми углами поворота относительно осей OX, OY, OZ, пересекающихся в центре С масс механической системы, состоящей из тел 2, 3, 4. При этих условиях главный момент  внешних сил относительно точки О равен нулю: (
внешних сил относительно точки О равен нулю: (  = 0). Кинетический момент LO гироскопа направлен по оси ОХ. Конец вектора LO обозначим точкой D (см. рис 7.7).
= 0). Кинетический момент LO гироскопа направлен по оси ОХ. Конец вектора LO обозначим точкой D (см. рис 7.7).
Применив теорему Резаля (U =  ), находим U = 0, т. е. скорость точки U равна нулю. Это означает, что при вращении массивного тела 2 ось ОХ гироскопа сохраняет неизменное положение в пространстве.
), находим U = 0, т. е. скорость точки U равна нулю. Это означает, что при вращении массивного тела 2 ось ОХ гироскопа сохраняет неизменное положение в пространстве.
Таким образом, ответ на вопрос, поставленный в задаче, получен.
§
При изменении положения оси гироскопа (рис. 7.8) формируется гироскопический момент  относительно точки О, который определяют по формуле
относительно точки О, который определяют по формуле
 = JO1Z1·
= JO1Z1·  ×
×  ,
,

где JO1Z1 – момент инерции гироскопа относительно оси O1Z1;  – вектор угловой скорости вращения гироскопа относительно оси O1Z1;
– вектор угловой скорости вращения гироскопа относительно оси O1Z1;  – вектор угловой скорости вращения гироскопа относительно оси прецессии OZ.
– вектор угловой скорости вращения гироскопа относительно оси прецессии OZ.
На рис. 7.8 оси OZ, O1Z1 расположены в плоскости OYZ. Согласно правилу векторного произведения вектор  одновременно перпендикулярен векторам
одновременно перпендикулярен векторам  ,
,  и направлен в сторону, откуда виден поворот вектора
и направлен в сторону, откуда виден поворот вектора  к вектору
к вектору  , происходящий против хода часовой стрелки. Исходя из этого правила, вектор
, происходящий против хода часовой стрелки. Исходя из этого правила, вектор  лежит на оси ОХ и направлен в сторону увеличения координаты Х. Модуль
лежит на оси ОХ и направлен в сторону увеличения координаты Х. Модуль 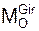 гироскопического момента определяют по формуле
гироскопического момента определяют по формуле
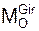 = JO1Z1·I
= JO1Z1·I  I·I
I·I  I = JO1Z1·ω·ω1·sin(θ),
I = JO1Z1·ω·ω1·sin(θ),
где ω = I  I, ω1 = I
I, ω1 = I  I – модули векторов
I – модули векторов  ,
,  ; θ – угол, составленный векторами
; θ – угол, составленный векторами  ,
,  .
.
Гироскопический момент  стремится совместить ось гироскопа с осью прецессии.
стремится совместить ось гироскопа с осью прецессии.

Рассмотрим быстрое вращение тела 1 с угловой скоростью  в рамке 2, которая вращается относительно угловой оси OY с угловой скоростью
в рамке 2, которая вращается относительно угловой оси OY с угловой скоростью  (рис. 7.9).
(рис. 7.9).
При этом выполняется неравенство I  I >> I
I >> I  I. По отношению к рамке 2 цилиндрические шарниры в точках А и В являются внешними связями. В этих связях формируются гироскопические (динамические) реакции RA, RB, противодействующие моменту
I. По отношению к рамке 2 цилиндрические шарниры в точках А и В являются внешними связями. В этих связях формируются гироскопические (динамические) реакции RA, RB, противодействующие моменту  . Реакции RA, RB образуют пару сил, алгебраический момент MSopr которой равен
. Реакции RA, RB образуют пару сил, алгебраический момент MSopr которой равен
MSopr = RA·h.
Вектор MSopr этой пары сил направлен противоположно вектору  гироскопического момента (рис. 7.10).
гироскопического момента (рис. 7.10).
Вектор MSopr момента реакций опор А и В и его модуль MSopr можно также определять по формулам:
MSopr = –  =
=  × JOХ·
× JOХ·  ·= – JOХ·
·= – JOХ·  ×
×  ;
;
MSopr = JOХ·ω·ω1·= – JOХ·I  I×I
I×I  I.
I.
Задачи на определение гироскопических реакций опор рекомендуется решать по следующему алгоритму.
1. Изобразить на рисунке векторы  угловой скорости собственного вращения гироскопа и его кинетического момента LO = JOХ·
угловой скорости собственного вращения гироскопа и его кинетического момента LO = JOХ·  .
.
2. Определить и изобразить на рисунке вектор  угловой скорости прецессии оси гироскопа.
угловой скорости прецессии оси гироскопа.
3. Найти гироскопический момент  и его модуль
и его модуль 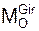 по формулам:
по формулам:  = JO1Z1·
= JO1Z1·  ×
×  ;
; 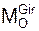 = JO1Z1·I
= JO1Z1·I  I·I
I·I  I = JO1Z1·ω·ω1·sin(θ),
I = JO1Z1·ω·ω1·sin(θ),
где ω = I  I, ω1 = I
I, ω1 = I  I – модули векторов
I – модули векторов  ,
,  ; θ – угол, составленный векторами
; θ – угол, составленный векторами  ,
,  .
.
4. Определить вектор MSopr момента реакций опор А и В и его модуль MSopr по формулам:
MSopr = –  =
=  × JOХ·
× JOХ·  ·= – JOХ·
·= – JOХ·  ×
×  ;
;
MSopr = JOХ·ω·ω1·= – JOХ·I  I×I
I×I  I.
I.
5. Определить модуль реакции одной из опор гироскопа по формуле RA = JOХ·ω·ω1/h.
УДАР
§
§
Примечание. Этот промежуток времени называют временем удара.
В теории удара классической механики вводится следующая идеализация этого процесса – совершается предельный переход к бесконечно большим силам, действующим бесконечно малое время (ударные силы) и имеющим конечный импульс S.
Ударная сила – сила, импульс которой за время удара является конечной величиной.
Ударный импульс – импульс ударной силы за время удара.
В технической литературе зачастую ударные силы называют мгновенными силами.
Согласно известным утверждениям кинематики поступательное движение твёрдого тела имеет такие же уравнения движения, как и точка. Рассмотрим движение материальной точки массой m в инерциальной системе отсчёта OXYZ под действием силы тяжести G и активной силы FiE на участке АВ (рис. 8.2).
В момент времени, когда материальная точка занимает на траектории её движения положение В, происходит удар. В этом положении материальная точка получает конечное изменение скорости от V1 до V2. В момент удара на материальную точку кроме сил G и FiE действует ударная сила Р. В отличие от ударной силы Р, силы FiE и G называют немгновенными силами.
В положении В, где действовала ударная сила Р, происходит резкое изменение траектории движения АВD точки. После прекращения действия ударной силы Р материальная точка на участке ВD снова движется под действием силы тяжести G и активной силы FiE.
Таким образом, в теории удара классической механики сделаны следующие допущения.
1. Действие немгновенных сил за время удара не учитывают.
2. Перемещение материальной точки за время удара не учитывают.
3. Результат действия ударной силы на материальную точку выражается в скачкообразном (конечном) изменении за время удара вектора её скорости, которое описывается векторным равенством V2 = V1 (S/m).

В действительности скачок скорости происходит в течение очень малого промежутка времени. Рассмотрим взаимодействие двух тел, совершающих поступательное движение в момент удара (рис. 8.3), и введём понятия, широко используемые в инженерной практике.
Линия центров – линия, проходящая через центры масс соударяющихся тел.
Центральный удар – удар, при котором линия действия ударного импульса, приложенного к ударяемому телу, проходит через его центр масс.
Прямой удар – удар, при котором скорости центров масс соударяющихся тел лежат на линии центров.
Косой удар – удар, при котором хотя бы одна из скоростей центров масс соударяющихся тел не лежит на линии центров.
Рассмотрение процесса удара требует выхода из рамок классической механики – отказа от схемы абсолютно твёрдого тела и перехода к схеме деформируемого тела. В зависимости от степени восстановления недеформированного состояния удары разделяются на абсолютно неупругие, упругие и абсолютно упругие.
Абсолютно неупругий удар – удар, при котором недеформированное состояние соударяющихся тел не восстанавливается.
В конце неупругого удара центры тяжести соударяющихся движутся с одинаковыми скоростями.
Упругий удар – удар, при котором недеформированное состояние тел восстанавливается не полностью.
В конце упругого удара центры тяжести соударяющихся тел движутся с разными скоростями.
Абсолютно упругий удар – удар, при котором недеформированное состояние соударяющихся тел восстанавливается полностью.
В конце абсолютно упругого удара центры тяжести соударяющихся тел движутся с разными скоростями.
Рассмотрим прямой центральный упругий удар двух тел. На рис. 8.4 изображена расчётная схема этого удара. До удара (см. рис. 8.4,а) соударяющиеся тела 1 и 2 движутся в одном направлении с абсолютными скоростями VC1, VC2 центров С1, С2 масс этих тел. На рис. 8.4,б изображен момент удара тел 1 и 2. Расчётная схема движения тел после удара приведена на рис. 8.4,в.
Напомним, что абсолютной скоростью называют скорость в инерциальной системе отсчёта.
Процесс упругого удара разделим на два этапа. В течение первого этапа (см. рис. 8.4,б) совершается деформация соударяющихся тел. В течение второго этапа – частичное восстановление недеформированного состояния. В момент окончания первого этапа и начала второго центры масс тел обладают одинаковыми скоростями, которые они имели бы в конце соответствующего абсолютно неупругого удара. В конце второго этапа центры масс тел имеют другие абсолютные скорости UС1, UС2.

Отношение изменений скоростей тел после удара к скоростям тел до удара характеризуется коэффициентом восстановления при ударе.
Коэффициент восстановления при ударе – величина, равная модулю отношения разности проекций скоростей центров масс тел на нормаль после удара к разности проекций скоростей центров масс тел на нормаль до удара.
Величину коэффициента k определяют по формуле
k = 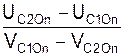 ,
,
где UC2On, UC1On – проекции абсолютных скоростей центров масс тел 2 и 1 на главную нормаль после удара; VC1On, VC2On – проекции абсолютных скоростей центров масс тел 1 и 2 до удара.
Коэффициент восстановления, являющийся безразмерной величиной, изменяется в пределах от 0 до 1 (0 < k < 1); при абсолютно неупругом ударе k = 0, при упругом ударе k < 1, при упругом ударе k = 1.
Рассмотрим косой центральный удар двух тел (рис. 8.5).
При рассмотрении косого центрального упругого удара поступательно движущихся твёрдых тел поверхности соударяющихся тел будем считать абсолютно гладкими.
До удара (см. рис. 8.5а) абсолютные скорости VC1, VC2 центров С1, С2 центров масс тел 1 и 2 направлены к линии центров под углами α1, α2. После удара (см. рис. 8.5,б) абсолютные скорости UC1, UC2 центров масс тел 1 и 2 направлены к линии центров под углами β1, β2.
Величину коэффициента k при косом ударе определяют по формуле
k = 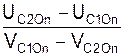 =
= 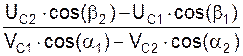 .
.
§
Рассмотрим удар поступательно движущегося шара о неподвижную плоскость (рис. 8.6).
Шар массой m движется поступательно и скорость VC направлена по нормали к неподвижной массивной поверхности в точке А. В момент времени, когда шар достигает этой поверхности, происходит прямой центральный удар. Различают две фазы этого удара. В течение первой фазы шар деформируется до тех пор, пока скорость его не станет равной нулю. Во время этой фазы кинетическая энергия шара обращается в потенциальную энергию сил упругости деформируемых тел и частично расходуется на их нагревание. В течение второй фазы под действием сил упругости шар частично восстанавливает свою первоначальную форму. Из-за остаточных деформаций и нагревания шара первоначальная кинетическая энергия шара полностью не восстанавливается. Поэтому шар отделяется от неподвижной поверхности с абсолютной скоростью UС, модуль которой меньше модуля его скорости VC до удара.
Согласно рис. 8.6, шар падает на неподвижную горизонтальную плоскость с высоты h1, при этом начальная скорость его центра масс равна нулю (VC0 = 0). В начале процесса удара скорость его центра масс равна VC. В конце удара шар со скоростью центра масс UС отрывается от неподвижной поверхности и поднимается на высоту h2max, где скорость его центра масс равна нулю.
По известным величинам h1, h2max определяют коэффициент восстановления при ударе по формуле
k = 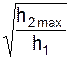 .
.
Эта формула используется при экспериментальном определении коэффициента восстановления.
В случае абсолютно неупругого удара шар от плоскости не отделяется, т е. h2 = 0. Тогда k = 0.
При абсолютно упругом ударе шар отскакивает от неподвижной плоскости и возвращается в исходное положение, т. е. h2max = h1. В этом случае k = 1.
При упругом ударе h2max < h1 и, следовательно, 0 < k < 1.
В случае прямого центрального удара тела о неподвижную поверхность модули скоростей связаны соотношением
UС = k·VC.
Рассмотрим косой удар шара о неподвижную горизонтальную плоскость (рис. 8.7).
Шар ударяется о неподвижную плоскость со скоростью VC, которая направлена к этой плоскости под углом α. После удара шар отскакивает от неподвижной плоскости со скоростью UС, под углом β к плоскости. Коэффициент восстановления при ударе определяют по формуле
k = 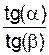 .
.
Последняя формула указывает удобный способ экспериментального определения коэффициента восстановления k при упругом ударе. По этому способу замеряют угол α и угол β отражения.
В случае абсолютно упругого удара угол падения α равен углу отражения β, откуда k = 1.
Задачи на определение коэффициента восстановления при ударе решают по следующему алгоритму.
1. Направить на рисунке главную нормаль (ось On) вдоль линии центров, а касательную (ось Оt) – перпендикулярно к ней.
2. Вычислить проекции скоростей VC1On, VC2On центров масс С1, С2 соударяющихся тел в начале удара на главную нормаль.
3. Вычислить проекции скоростей UC1On, UC2On центров масс С1, С2 соударяющихся тел в конце удара на главную нормаль.
4. Определить коэффициент восстановления при ударе по формуле k = 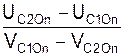 .
.
§
Из–за остаточных деформаций и нагревания тел при ударе происходит частичная потеря кинетической энергии соударяющихся тел. Определим потерю кинетической энергии при упругом ударе двух поступательно движущихся тел, имеющих коэффициент восстановления k.
Введём условные обозначения: Т1 – кинетическая энергия механической системы до удара; Т2 – кинетическая энергия механической системы после удара; ΔТ – потеря кинетической энергии механической системы в процессе удара.
Величины Т1, Т2, ΔТ определяют по формулам:
T1 = 0,5·(m1·(VC1)2 m2·(VC2)2);
T1 = 0,5·(m1·(UC1)2 m2·(UC2)2);
ΔT = T1 – T2,
где m1, m2 – массы соударяющихся тел; VC1, VC2 – модули абсолютных скоростей центров масс тел до удара; UC1, UC2 – модули абсолютных скоростей центров масс тел после удара.
Потерю кинетической энергии при прямом центральном упругом ударе определяют по формуле
ΔT = (1 – k2)· 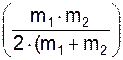 ·(VC1On – VC2On)2,
·(VC1On – VC2On)2,
где VC1On, VC2On – проекции абсолютных скоростей центров масс тел 1, 2 на главную нормаль.
При абсолютно неупругом ударе k = 0 и, следовательно,
ΔT = 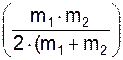 ·(VC1On – VC2On)2.
·(VC1On – VC2On)2.
При абсолютно упругом ударе k = 1 и, следовательно, ΔT = 0.
Решение задач на вычисление потери кинетической энергии при ударе двух тел следует выполнять по приведённым выше формулам.
§

Рассмотрим процесс удара при вращении твёрдого тела на примере плоской пластины под действием активных сил FiE и реакций RiE внешних связей в инерциальной системе отсчёта OXYZ (рис. 8.8).
Твёрдое тело до удара вращается относительно оси ОХ с угловой скоростью  . В момент удара о неподвижную поверхность (см. рис. 8.8,а) твёрдое тело имело угловую скорость
. В момент удара о неподвижную поверхность (см. рис. 8.8,а) твёрдое тело имело угловую скорость 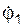 , а после удара его угловая скорость изменилась до значения
, а после удара его угловая скорость изменилась до значения 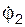 (см. рис. 8.8,в).
(см. рис. 8.8,в).
Напомним, что по теории удара силы FiE, RiE являются немгновенными силами, следовательно, их действие на твёрдое тело не учитывается.
В момент удара на тело действуют ударные силы РiE, ударный импульс которых обозначим символом S(PiE) (см. рис. 8.8,б). Ударные силы РiE относятся к разряду внешних сил.
Определим изменение угловой скорости тела в момент удара. Для этого воспользуемся выражением
LOX(2) – LOX(1) = ΣMOX(S(PiE)),
где LOX(1), LOX(2) – кинетические моменты тела относительно оси ОХ вращения до и после удара; ΣMOX(S(PiE)) – сумма моментов ударных импульсов относительно оси вращения тела.
Последняя формула выражает теорему об изменении кинетического момента механической системы при ударе.
Изменение кинетического момента механической системы относительно оси вращения при ударе равно сумме моментов внешних ударных импульсов, приложенных к точкам системы, относительно той же оси.
Кинетический момент твёрдого тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на модуль угловой скорости. Исходя из этого, имеем:
LOX(1) = JOX·I 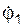 I; LOX(1) = JOX·I
I; LOX(1) = JOX·I 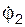 I.
I.
Тогда теорему об изменении кинетического момента механической системы относительно оси вращения при ударе можно представить в следующем виде:
JOX·I 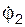 I – JOX·I
I – JOX·I 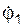 I = ΣMOX(S(PiE)).
I = ΣMOX(S(PiE)).
Отсюда
Δφ = I 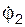 I – I
I – I 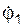 I =
I = 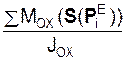 .
.
Таким образом, изменение угловой скорости твёрдого тела, вращающегося относительно неподвижной оси, под действием внешних ударных сил равно сумме моментов импульсов этих сил относительно оси вращения, разделённой относительно той же оси.
Итак, действие ударного импульса на тело, вращающегося относительно неподвижной оси, проявляется в скачкообразном изменении его угловой скорости.
Этой теоремой следует пользоваться в задачах на удар по телу, вращающемуся относительно неподвижной оси, когда в число данных и искомых величин входят: ударные импульсы; момент инерции тела относительно оси вращения; угловые скорости в начале и конце удара.
Задачи с помощью теоремы об изменении кинетического момента механической системы при ударе решают по следующему алгоритму.
1. Изобразить на рисунке внешние ударные импульсы.
2. Вычислить сумму моментов ударных импульсов относительно оси вращения.
3. Подставив результат вычислений, полученный в предыдущем пункте, в уравнение Δφ = I 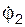 I – I
I – I 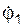 I =
I = 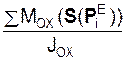 , определить искомую величину.
, определить искомую величину.
