- Гибкие валы и булавы для вибраторов
- Голономная система (физика)
- Дифференциальная форма
- Жесткое тело
- Классификация связей: голономные, стационарные и удерживающие. виртуальное перемещение точки. виртуальная работа. идеальная связь.
- Классификация физических систем
- Маятник
- Преобразование в независимые обобщенные координаты
Гибкие валы и булавы для вибраторов
Важными деталями вибратора для уплотнения бетона являются гибкий вал для глубинного вибратора и вибробулава, или вибронаконечник. Вал играет роль передатчика колебаний вибронаконечнику, который погружается в бетон и передает общей массе импульсы, удаляющие все пустоты и пузырьки воздуха.
Все гибкие валы различаются по двум характеристикам:

диаметру, влияющему на общую площадь обрабатываемого бетона, и длине, связанной со сферой использования, например:
К выбору булавы для вибратора также нужно отнестись с должным вниманием: от этого зависит, сможете ли вы обработать нужную вам бетонную поверхность. Следует учесть длину вибробулавы, от которой зависит толщина уложенного бетона, и диаметр, который влияет на тип обрабатываемой поверхности.
На нашем сайте представлены вибронаконечники диаметром от 25 мм, как у вибробулавы Wacker Neuson H 25 5000006567, до 76 мм, как у вибронаконечника Красный Маяк 045-0340. Для примера диаметр 38 и 28 мм используется для узких и труднодоступных мест, залитых бетоном: стен, колонн, различных перекрытий, а вибронаконечник d 51 мм, как и вибронаконечник 76 мм, используется в основном для уплотнения залитых фундаментов.
Оформление заказа на нужную вам булаву для вибратора или гибкий вал займет не более 10 минут. Вам надо позвонить по телефону 8-800-333-83-28 (звонок по России бесплатный) или же оформить заказ через Личный кабинет. Более подробную информацию о преимуществах товара и сроках доставки вам расскажет менеджер.
§
§
Голономная система (физика)
В классической механике систему можно определить как голономную, если все связи системы голономны. Чтобы ограничение было голономным, оно должно быть выражено как функция :
- ж(Икс1, Икс2, Икс3, …, ИксN, т)знак равно0,{ Displaystyle е (x_ {1}, x_ {2}, x_ {3}, ldots, x_ {N}, t) = 0, ,}
т.е. голономная связь зависит только от координат и времени . Он не зависит от скоростей или какой-либо производной более высокого порядка по t . Ограничение, которое не может быть выражено в форме, показанной выше, является неголономным ограничением .
Иксj{ Displaystyle х_ {j} , !}т{ Displaystyle т , !}
Дифференциальная форма
Рассмотрим следующую дифференциальную форму уравнения связи:
- ∑j cяjdqj cяdтзнак равно0;{ Displaystyle сумма _ {j} c_ {ij} , dq_ {j} c_ {i} , dt = 0; ,}
где c ij , c i – коэффициенты дифференциалов dq j и dt для i- го ограничения.
Если дифференциальная форма интегрируема, т. Е. Если существует функция, удовлетворяющая равенству
жя(q1, q2, q3, …, qN, т)знак равно0{ Displaystyle f_ {я} (q_ {1}, q_ {2}, q_ {3}, ldots, q_ {N}, t) = 0 , !}
- dжязнак равно∑j cяjdqj cяdтзнак равно0,{ displaystyle df_ {i} = sum _ {j} c_ {ij} , dq_ {j} c_ {i} , dt = 0, ,}
тогда это ограничение является голономным; в противном случае неголономный. Следовательно, все голономные и некоторые неголономные связи могут быть выражены с помощью дифференциальной формы. Не все неголономные связи можно выразить таким образом. Примеры неголономных связей, которые нельзя выразить таким образом, – это те, которые зависят от обобщенных скоростей.
Жесткое тело
Частицы твердого тела подчиняются голономной связи
- (ря-рj)2-Lяj2знак равно0,{ displaystyle ( mathbf {r} _ {i} – mathbf {r} _ {j}) ^ {2} -L_ {ij} ^ {2} = 0, ,}
где , – соответственно положения частиц и , – расстояние между ними.
ря{ displaystyle mathbf {r} _ {i} , !}рj{ Displaystyle mathbf {r} _ {j} , !}пя{ Displaystyle P_ {я} , !}пj{ Displaystyle P_ {j} , !}Lяj{ Displaystyle L_ {ij} , !}
Классификация связей: голономные, стационарные и удерживающие. виртуальное перемещение точки. виртуальная работа. идеальная связь.
Связь называется голономной, если в уравнение связи входят только координаты точек механической системы или иные параметры, определяющие ее положение в пространстве. 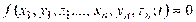
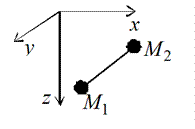
Связь называют удерживающей, если она выражается математически равенством, и неудерживающей, если она выражается неравенством.
Связь называется стационарной, если в уравнение связи время явно не входит. Если в уравнение связи время входит явным образом, то связь − нестационарная.
Примером нестационарной связи, наложенной на материальную точку, является нить, длина которой изменяется согласно некоторому закону  . Это голономная, неудерживающая, нестационарная связь.
. Это голономная, неудерживающая, нестационарная связь.
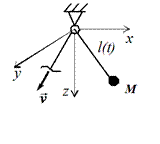
Виртуальным (возможным) перемещением точки (обозначается 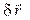 ) называется такое бесконечно малое (элементарное) перемещение, которое допускается в рассматриваемый момент движения наложенными на точку связями.
) называется такое бесконечно малое (элементарное) перемещение, которое допускается в рассматриваемый момент движения наложенными на точку связями.
Проекции вектора виртуального перемещения точки 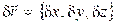 называются вариациями координат.
называются вариациями координат.
В случае голономной нестационарной связи уравнение 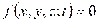 в фиксированный момент определяет некоторую поверхность в трехмерном пространстве, на которой находится движущаяся точка. Виртуальные перемещения лежат в касательной плоскости к этой поверхности и вариации координат удовлетворяют уравнению
в фиксированный момент определяет некоторую поверхность в трехмерном пространстве, на которой находится движущаяся точка. Виртуальные перемещения лежат в касательной плоскости к этой поверхности и вариации координат удовлетворяют уравнению 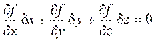 ,
,
выражающему перпендикулярность вектора нормали к поверхности 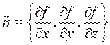 и вектора
и вектора 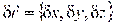 .
.
Виртуальным перемещением механической системы называется совокупность виртуальных перемещений точек этой системы.
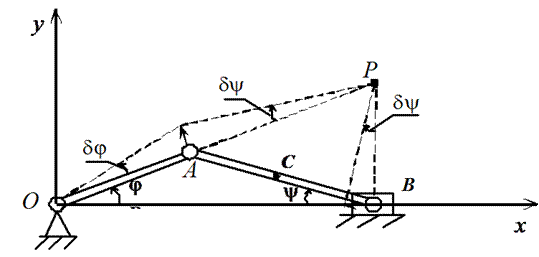
Например, виртуальным перемещением кривошипно-ползунного механизма, являются два элементарных поворота – кривошипа на угол 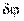 вокруг оси вращения и шатуна на угол
вокруг оси вращения и шатуна на угол 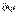 вокруг мгновенного центра скоростей. Из геометрических соображений следует, что:
вокруг мгновенного центра скоростей. Из геометрических соображений следует, что:  . Связь между виртуальными перемещениями отдельных тел и точек, образующих механическую систему, в общем случае может быть найдена аналитически путем варьирования уравнений связи.
. Связь между виртуальными перемещениями отдельных тел и точек, образующих механическую систему, в общем случае может быть найдена аналитически путем варьирования уравнений связи.
Виртуальной работой силы(обозначается 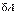 )называется работа силы на виртуальном перемещении точки ее приложения, т.е.:
)называется работа силы на виртуальном перемещении точки ее приложения, т.е.:  .
.
Связь называется идеальной, если сумма работ реакций этой связи на любом виртуальном перемещении системы равна нулю.
 Примером является шероховатая поверхность для катка, катящегося без скольжения, при отсутствии трения качения
Примером является шероховатая поверхность для катка, катящегося без скольжения, при отсутствии трения качения 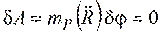 .
.
Принцип виртуальных перемещений.
Для равновесия механической системы с идеальными и стационарными связями необходимо и достаточно, чтобы сумма виртуальных работ всех активных сил, приложенных к точкам системы, была равна нулю
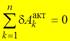
Дано, что механическая система находится в равновесии и требуется доказать, что  . Так как система находится в равновесии, то равнодействующая активных сил
. Так как система находится в равновесии, то равнодействующая активных сил  и равнодействующая сил реакций связей
и равнодействующая сил реакций связей 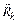 , приложенных в
, приложенных в 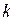 -й точке системы, удовлетворяют условию равновесия статики:
-й точке системы, удовлетворяют условию равновесия статики:
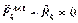 ,
, 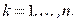
Пусть  , докажем, что механическая система находится в равновесии. Предположим, что при заданных условиях система не находится в равновесии, т. е. при действии на систему активных сил хотя бы одна точка получила действительное перемещение
, докажем, что механическая система находится в равновесии. Предположим, что при заданных условиях система не находится в равновесии, т. е. при действии на систему активных сил хотя бы одна точка получила действительное перемещение 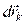 и
и 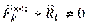 .
.
Так как для стационарных связей действительное перемещение совпадает с одним из возможных (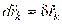 ), то
), то  или
или 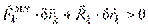 по крайней мере для одной точки системы, вышедшей из равновесия. Суммируя по всем точкам системы, получаем
по крайней мере для одной точки системы, вышедшей из равновесия. Суммируя по всем точкам системы, получаем 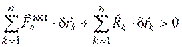 .
.
Так как связи идеальные, то 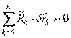 Þ
Þ 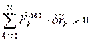 Þ
Þ 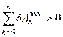 , что противоречит условию.
, что противоречит условию.
Следовательно, система находится в равновесии.
Принцип виртуальных перемещений может быть записан в иной форме, если поделить уравнение, выражающее этот принцип на временной интервал 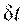 , в течение которого совершается это перемещение.
, в течение которого совершается это перемещение.
Общее уравнение динамики.
Рассмотрим систему, состоящую из N материальных точек, с идеальными и голономными связями, положение которой однозначно определяется s обобщенными координатами 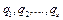 . Запишем для каждой точки системы основное уравнение динамики
. Запишем для каждой точки системы основное уравнение динамики
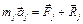
или
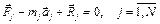 .
.
Зафиксируем время и дадим системе виртуальное перемещение, при котором радиус-векторы точек получат приращения 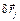 . Умножим скалярно каждое уравнение на
. Умножим скалярно каждое уравнение на 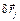 и сложим полученные произведения
и сложим полученные произведения
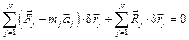
Так как связи идеальные, последняя сумма равна нулю и из уравнения получим
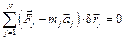
Учитывая, что 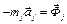 – это сила инерции j-й материальной точки,
– это сила инерции j-й материальной точки, 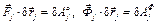 – работы активной силы и силы инерции, перепишем равенство в виде:
– работы активной силы и силы инерции, перепишем равенство в виде:
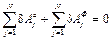 .
.
Это уравнение называют общим уравнением динамики. Оно утверждает, что при движении системы с идеальными связями в любой момент времени сумма работ активных сил и сил инерции на любом виртуальном перемещении системы равна нулю.
Классификация физических систем
Чтобы изучать классическую физику строго и методично, нам необходимо классифицировать системы. Основываясь на предыдущем обсуждении, мы можем классифицировать физические системы на голономные системы и неголономные системы . Одним из условий применимости многих теорем и уравнений является то, что система должна быть голономной системой.
Маятник

Простой маятник
Как показано справа, простой маятник представляет собой систему, состоящую из груза и веревки. Трос прикреплен на верхнем конце к оси, а на нижнем конце к грузу. Длина строки нерастяжима, поэтому она постоянна. Следовательно, эта система голономна; он подчиняется голономной связи
- Икс2 y2-L2знак равно0,{ displaystyle {x ^ {2} y ^ {2}} – L ^ {2} = 0,}
где – положение груза, а – длина струны.
(Икс, y){ Displaystyle (х, у) , !}L{ Displaystyle L , !}
Преобразование в независимые обобщенные координаты
Уравнения голономных связей могут помочь нам легко удалить некоторые зависимые переменные в нашей системе. Например, если мы хотим удалить параметр в уравнении ограничения , мы можем преобразовать уравнение в следующую форму, предполагая, что это можно сделать,
Иксd{ displaystyle x_ {d} , !}жя{ displaystyle f_ {i} , !}
- Иксdзнак равнограммя(Икс1, Икс2, Икс3, …, Иксd-1, Иксd 1, …, ИксN, т),{ Displaystyle x_ {d} = g_ {i} (x_ {1}, x_ {2}, x_ {3}, dots, x_ {d-1}, x_ {d 1}, точки, x_ {N}, t), ,}
и замените в каждом уравнении системы указанную выше функцию. Это всегда можно сделать для общей физической системы, при условии , что есть , то по теореме о неявной функции , решение гарантировано в некотором открытом множестве. Таким образом, можно удалить все вхождения зависимой переменной .
Иксd{ displaystyle x_ {d} , !}жя{ displaystyle f_ {i} , !}C1{ Displaystyle С ^ {1} , !}граммя{ displaystyle g_ {i} ,}Иксd{ displaystyle x_ {d} , !}Предположим, что у физической системы есть степени свободы. Теперь на систему накладываются голономные ограничения. Затем количество степеней свободы уменьшается до . Мы можем использовать независимые обобщенные координаты ( ), чтобы полностью описать движение системы. Уравнение преобразования можно выразить следующим образом:
N{ Displaystyle N , !}час{ Displaystyle ч , !}мзнак равноN-час{ displaystyle m = Nh , !}м{ Displaystyle м , !}qj{ displaystyle q_ {j} , !}
- Иксязнак равноИкся(q1, q2, …, qм, т) ,язнак равно1, 2, …N.{ displaystyle x_ {i} = x_ {i} (q_ {1}, q_ {2}, ldots, q_ {m}, t) , qquad qquad qquad i = 1, 2, ldots N. ,}





























